Question

12．若a和b是计算机在区间（0，2）上产生的随机数，那么函数f（x）=lg（ax²+4x+4b）的定义域为R（实数集）的概率为（　　）

• A． $\frac{3-2ln2}{4}$
• B． $\frac{1+2ln2}{4}$
• C． $\frac{1+ln2}{2}$
• D． $\frac{1-ln2}{2}$

Answer 1

分析 运用函数f（x）=lg（ax²+4x+4b）的值域为R（实数集），求出a，b的范围，再由几何概概型的概率公式，即可得到．

解答 解：由已知，a和b是计算机在区间（0，2）上产生的随机数，对应区域的面积为4，
要函数f（x）=lg（ax²+4x+4b）的定义域为R（实数集），则（ax²+4x+4b）恒为正，
∴△=16-16ab＜0，即ab＞1；
在平面直角坐标系中画出点（a，b）所在区域：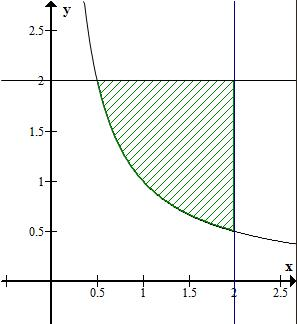

满足ab＞1的区域面积为：${∫}_{\frac{1}{2}}^{2}（2-\frac{1}{x}）dx$=3-2ln2；
∴所求概率为P=$\frac{3-2ln2}{4}$；
故选A

点评 本题考查的知识点是几何概型公式的运用，关键是要找出（0，2）上产生两个随机数a和b所对就图形的面积；
几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．