
 如图,在矩形ABCD中,AB=2,AD=1,在平面内将矩形ABCD绕点B按顺时针方向旋转60°后得到矩形A′BC′D′,则点D′到直线AB的距离是$\sqrt{3}+\frac{1}{2}$.
如图,在矩形ABCD中,AB=2,AD=1,在平面内将矩形ABCD绕点B按顺时针方向旋转60°后得到矩形A′BC′D′,则点D′到直线AB的距离是$\sqrt{3}+\frac{1}{2}$. 分析 画出图形,利用三角函数的关系,通过两角和的正弦函数以及同角三角函数的基本关系式求解即可.
解答  解:连结BD,D′B,设∠DBA=α,由题意可知:BD=$\sqrt{5}$,D′B=$\sqrt{5}$.
解:连结BD,D′B,设∠DBA=α,由题意可知:BD=$\sqrt{5}$,D′B=$\sqrt{5}$.
tan$α=\frac{1}{2}$,
∠D′BA=α+60°,sin2(α+60°)=(sinαcos60°+cosαsin60°)2=($\frac{1}{2}$sinα+$\frac{\sqrt{3}}{2}$cosα)2
=$\frac{1}{4}{sin}^{2}α+\frac{\sqrt{3}}{2}sinαcosα+\frac{3}{4}{cos}^{2}α$
=$\frac{\frac{1}{4}{sin}^{2}α+\frac{\sqrt{3}}{2}sinαcosα+\frac{3}{4}{cos}^{2}α}{{sin}^{2}α+{cos}^{2}α}$
=$\frac{\frac{1}{4}{tan}^{2}α+\frac{\sqrt{3}}{2}tanα+\frac{3}{4}}{{tan}^{2}α+1}$
=$\frac{\frac{1}{4}×(\frac{1}{2})^{2}+\frac{\sqrt{3}}{2}×\frac{1}{2}+\frac{3}{4}}{{(\frac{1}{2})}^{2}+1}$=$\frac{2\sqrt{3}+1}{2\sqrt{5}}$.
点D′到直线AB的距离:
∴sin(α+60°)=$\frac{2\sqrt{3}+1}{2\sqrt{5}}×\sqrt{5}$=$\sqrt{3}+\frac{1}{2}$,
故答案为:$\sqrt{3}+\frac{1}{2}$.
点评 本题考查三角形中的基本运算,两角和的正弦函数的应用,考查计算能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3-2ln2}{4}$ | B. | $\frac{1+2ln2}{4}$ | C. | $\frac{1+ln2}{2}$ | D. | $\frac{1-ln2}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图某综艺节目现场设有A,B,C,D四个观众席,现有由3不同颜色与2种不同款式组成的6种马甲安排给现场观众,要求每个观众席上的马甲相同,相邻观众席上的马甲的颜色与款式都不相同,则不同的安排方法种数为36.
如图某综艺节目现场设有A,B,C,D四个观众席,现有由3不同颜色与2种不同款式组成的6种马甲安排给现场观众,要求每个观众席上的马甲相同,相邻观众席上的马甲的颜色与款式都不相同,则不同的安排方法种数为36.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{1}{10}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
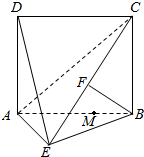 如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点.且BF⊥平面ACE.
如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点.且BF⊥平面ACE.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 9 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com