
(本小题满分13分)已知曲线C: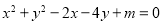 ,O为坐标原点
,O为坐标原点
(Ⅰ)当m为何值时,曲线C表示圆;
(Ⅱ)若曲线C与直线 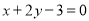 交于M、N两点,且OM⊥ON,求m的值.
交于M、N两点,且OM⊥ON,求m的值.
(Ⅰ)m<5;(Ⅱ)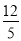 .
.
【解析】
试题分析:(Ⅰ)根据曲线方程满足圆的条件求出m的范围即可;
(Ⅱ)设M(x1,y1),N(x2,y2),由题意OM⊥ON,得到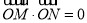 ,利用平面向量数量积运算法则列出关系式,联立直线与圆方程组成方程组,消去x得到关于y的一元二次方程,根据直线与圆有两个交点,得到根的判别式大于0,求出m的范围,利用韦达定理求出y1+y2与y1y2,由点M(x1,y1),N(x2,y2)在直线x+2y﹣3=0上,表示出x1与x2,代入得出的关系式中,整理即可确定m的值.
,利用平面向量数量积运算法则列出关系式,联立直线与圆方程组成方程组,消去x得到关于y的一元二次方程,根据直线与圆有两个交点,得到根的判别式大于0,求出m的范围,利用韦达定理求出y1+y2与y1y2,由点M(x1,y1),N(x2,y2)在直线x+2y﹣3=0上,表示出x1与x2,代入得出的关系式中,整理即可确定m的值.
试题解析:
【解析】
(Ⅰ)由题意可知:D2+E2﹣4F=(﹣2)2+(﹣4)2﹣4m=20﹣4m>0,
解得:m<5;
(Ⅱ)设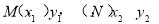 ,
,
由题意OM⊥ON,得到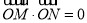 ,即:
,即: 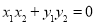 ①,
①,
联立直线方程和圆的方程:  ,
,
消去x得到关于y的一元二次方程: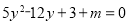 ,
,
∵直线与圆有两个交点,
∴△=b2﹣4ac=122﹣4×5×m>0,即m+3<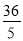 ,即m<
,即m<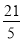 ,
,
又由(Ⅰ)m<5,∴m<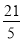 ,
,
由韦达定理: 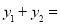
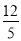 ,
,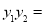
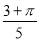 ②,
②,
又点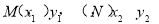 在直线
在直线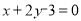 上,
上,
∴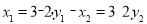 ,
,
代入①式得: 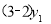
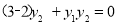 ,即
,即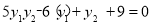 ,
,
将②式代入上式得到:3+m﹣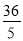 +9=0,
+9=0,
解得:m=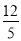 <
<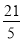 ,
,
则m=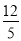 .
.
考点:①直线与圆的位置关系;②根的判别式;③直线与圆的交点;④韦达定理;⑤平面向量的数量积运算.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源:2014-2015学年江苏省高二上学期期中考试数学试卷(解析版) 题型:填空题
已知抛物线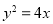 与双曲线
与双曲线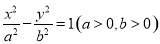 有相同的焦点
有相同的焦点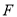 ,点
,点 是两曲线的一个交点,且
是两曲线的一个交点,且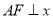 轴,则双曲线的离心率为 .
轴,则双曲线的离心率为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省高二上学期期中考试文科数学试卷(解析版) 题型:填空题
已知P是直线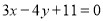 上的动点,PA,PB是圆
上的动点,PA,PB是圆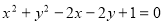 的切线,
的切线,
A,B是切点,C是圆心,那么四边形PACB的面积的最小值是___________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省高二上学期期中考试文科数学试卷(解析版) 题型:选择题
过点(1,2)总可以作两条直线与圆 相切,则
相切,则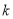 的取值范围是( )
的取值范围是( )
A.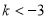 或
或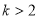
B.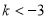 或
或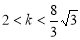
C.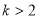 或
或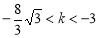
D.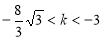 或
或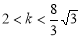
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
下列各组对象不能构成一个集合的是( )
| A.不超过20的非负实数 |
B.方程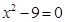 在实数范围内的解 在实数范围内的解 |
C. 的近似值的全体 的近似值的全体 |
| D.赣县中学北区2014年在校身高超过170厘米的同学 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com