
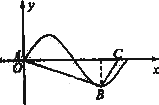
 已知函数f(x)=sinωx(ω>0)的一段图象如图所示,△ABC的顶点A与坐标原点O重合,B是f(x)的图象上一个最低点,C在x轴上,若内角A,B,C所对边长为a,b,c,且△ABC的面积S满足12S=b2+c2-a2,将f(x)右移一个单位得到g(x),则g(x)的表达式为( )
已知函数f(x)=sinωx(ω>0)的一段图象如图所示,△ABC的顶点A与坐标原点O重合,B是f(x)的图象上一个最低点,C在x轴上,若内角A,B,C所对边长为a,b,c,且△ABC的面积S满足12S=b2+c2-a2,将f(x)右移一个单位得到g(x),则g(x)的表达式为( )A、g(x)=cos(
| ||||
B、g(x)=-cos(
| ||||
C、g(x)=sin(
| ||||
D、g(x)=sin(
|
| 1 |
| 2 |
| 1 |
| 2 |
| 3T |
| 4 |
| 3T |
| 4 |
| 2π |
| ω |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |


科目:高中数学 来源: 题型:
| π |
| 6 |
| π |
| 6 |
| A、p∧q | B、p∧¬q |
| C、¬p∧q | D、¬p∨¬q |
查看答案和解析>>
科目:高中数学 来源: 题型:
| b+1 |
| b+2 |
| A、0 | ||
B、
| ||
C、-
| ||
| D、-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
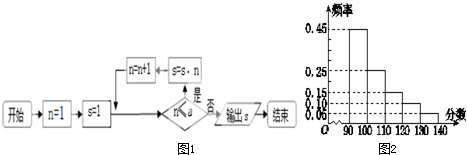
| A、800! | B、810! |
| C、811! | D、812! |
查看答案和解析>>
科目:高中数学 来源: 题型:
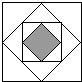 任意画一个正方形,再将这个正方体各边的中点相连得到第二个正方形,依此类推,这样一共画了4个正方形,如图所示.若向图形中随机投一点,则所投点落在第四个正方形的概率是( )
任意画一个正方形,再将这个正方体各边的中点相连得到第二个正方形,依此类推,这样一共画了4个正方形,如图所示.若向图形中随机投一点,则所投点落在第四个正方形的概率是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com