
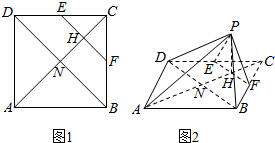
 如图1,正方形ABCD的边长为$2\sqrt{2}$,E、F分别是DC和BC的中点,H是正方形的对角线AC与EF的交点,N是正方形两对角线的交点,现沿EF将△CEF折起到△PEF的位置,使得PH⊥AH,连结PA,PB,PD(如图2).
如图1,正方形ABCD的边长为$2\sqrt{2}$,E、F分别是DC和BC的中点,H是正方形的对角线AC与EF的交点,N是正方形两对角线的交点,现沿EF将△CEF折起到△PEF的位置,使得PH⊥AH,连结PA,PB,PD(如图2).分析 (1)由PH⊥AH,PH⊥EF可得PH⊥平面ABCD,故PH⊥BD,又AC⊥BD,得出BD⊥平面PAH,得出BD$⊥AP\$;
(2)分别把△ABD和△BDP当做底面求出棱锥的体积,列出方程解出.
解答 (Ⅰ)证明:∵E、F分别是CD和BC的中点,∴EF∥BD.
又∵AC⊥BD,∴AC⊥EF,故折起后有PH⊥EF.
又∵PH⊥AH,∴PH⊥平面ABFED.
又∵BD?平面ABFED,∴PH⊥BD,
∵AH∩PH=H,AH,PH?平面APH,
∴BD⊥平面APH,又∵AP?平面APH,∴BD⊥AP
(Ⅱ)解:∵正方形ABCD的边长为$2\sqrt{2}$,
∴AC=BD=4,AN=2,NH=PH=1,PE=PF
∴△PBD是等腰三角形,连结PN,则PN⊥BD,$PN=\sqrt{N{H^2}+P{H^2}}=\sqrt{2}$
∴△PBD的面积${S_{△PBD}}=\frac{1}{2}BD•PN=\frac{1}{2}×4×\sqrt{2}=2\sqrt{2}$
设三棱锥A-BDP的高为h,则三棱锥A-BDP的体积为${V_{A-BDP}}=\frac{1}{3}{S_{△PBD}}•h=\frac{{2\sqrt{2}h}}{3}$
由(Ⅰ)可知PH是三棱锥P-ABD的高,∴三棱锥P-ABD的体积:${V_{P-ABD}}=\frac{1}{3}{S_{△ABD}}•PH=\frac{1}{3}×\frac{1}{2}AB•AD•PH=\frac{1}{3}×\frac{1}{2}×2\sqrt{2}×2\sqrt{2}×1=\frac{4}{3}$
∵VA-BDP=VP-ABD,即$\frac{{2\sqrt{2}h}}{3}=\frac{4}{3}$,解得$h=\sqrt{2}$,即三棱锥A-BDP的高为$\sqrt{2}$.
点评 本题考查了线面垂直的判定与性质,棱锥的体积计算,选择恰当的底面和高是计算体积的关键.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{{6+\sqrt{2}+\sqrt{6}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{3+\sqrt{2}+\sqrt{6}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com