
分析 由旋转变换公式可得:$(\begin{array}{l}{{x}^{′}}\\{{y}^{′}}\end{array})$=$(\begin{array}{l}{cos\frac{π}{2}}&{-sin\frac{π}{2}}\\{sin\frac{π}{2}}&{cos\frac{π}{2}}\end{array})$$(\begin{array}{l}{x}\\{y}\end{array})$,可得:$\left\{\begin{array}{l}{x={y}^{′}}\\{y=-{x}^{′}}\end{array}\right.$,代入椭圆方程即可得出.
解答 解:由旋转变换公式可得:$(\begin{array}{l}{{x}^{′}}\\{{y}^{′}}\end{array})$=$(\begin{array}{l}{cos\frac{π}{2}}&{-sin\frac{π}{2}}\\{sin\frac{π}{2}}&{cos\frac{π}{2}}\end{array})$$(\begin{array}{l}{x}\\{y}\end{array})$,可得:$\left\{\begin{array}{l}{x={y}^{′}}\\{y=-{x}^{′}}\end{array}\right.$,
代入椭圆方程可得:$\frac{({y}^{′})^{2}}{25}+$$\frac{(-{x}^{′})^{2}}{9}$=1,
即$\frac{{y}^{2}}{25}+\frac{{x}^{2}}{9}$=1,
故答案为:$\frac{{y}^{2}}{25}+\frac{{x}^{2}}{9}$=1.
点评 本题考查了旋转变换公式、椭圆的标准方程,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
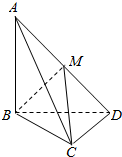 如图,三棱锥A-BCD中,AB=BD=CD=1,AD=BC=$\sqrt{2}$,AC=$\sqrt{3}$.
如图,三棱锥A-BCD中,AB=BD=CD=1,AD=BC=$\sqrt{2}$,AC=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
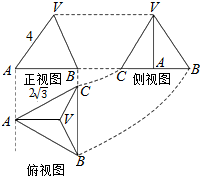
| A. | $\sqrt{39}$ | B. | 6$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)中,F1,F2分别是椭圆的左右焦点,点B(0,-b)是椭圆C的下顶点,BF1的延长线交椭圆C于点A,点D和点A关于x轴对称.
如图所示,在椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)中,F1,F2分别是椭圆的左右焦点,点B(0,-b)是椭圆C的下顶点,BF1的延长线交椭圆C于点A,点D和点A关于x轴对称.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
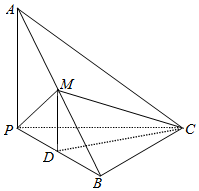 如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
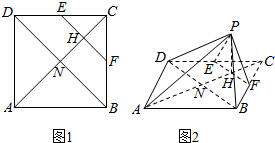 如图1,正方形ABCD的边长为$2\sqrt{2}$,E、F分别是DC和BC的中点,H是正方形的对角线AC与EF的交点,N是正方形两对角线的交点,现沿EF将△CEF折起到△PEF的位置,使得PH⊥AH,连结PA,PB,PD(如图2).
如图1,正方形ABCD的边长为$2\sqrt{2}$,E、F分别是DC和BC的中点,H是正方形的对角线AC与EF的交点,N是正方形两对角线的交点,现沿EF将△CEF折起到△PEF的位置,使得PH⊥AH,连结PA,PB,PD(如图2).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com