练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在△ABC中，a＝3，b＝2，∠B＝2∠A.

    (1)求cos A的值；

    (2)求c的值．


    (1)因为a＝3，b＝2，∠B＝2∠A，

    所以在△ABC中，由正弦定理得＝，

    所以＝，故cosA＝.

    (2)由(1)知cosA＝，

    所以sinA＝＝.

    又因为∠B＝2∠A，所以cosB＝2cos2A－1＝.

    所以sinB＝＝，

    在△ABC中，sinC＝sin(A＋B)

    ＝sinAcosB＋cosAsinB＝.

    所以c＝＝5.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知满足以下约束条件，则z=x2+y2的最大值和最小值分别是(    )

    　A.,1      B.13,1　    C.,      D.13,

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知定义在R上的函数y=f(x) 对于任意的x都满足f(x+1) =-f(x), 当

    -1≤x< 1时, , 若函数至少有6个零点, 则a的取值范围是(　　)

    A.∪(5, +∞)　　B.∪[5, +∞)　　C. ∪(5,7)　　D.∪[5,7)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝的定义域为(　　)

    A．(0，)   B．(2，＋∞)

    C．(0，)∪(2，＋∞)       D．(0，]∪[2，＋∞)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设f(x)是定义在R上的函数，若f(0)＝2008，且对任意x∈R，满足f(x＋2)－f(x)≤3·2x，f(x＋6)－f(x)≥63·2x，则f(2008)＝(　　)

    A．22006＋2007       B．22008＋2006

    C．22008＋2007 D．22006＋2008

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝a·2x＋b·3x，其中常数a、b满足a·b≠0.

    (1)若a·b>0，判断函数f(x)的单调性；

    (2)若a·b<0，求f(x＋1)>f(x)时的x的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：



    设等比数列的前项和为，若，，则（ ）

    A．17 B．33 C．-31 D．-3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


           已知函数

        （1）解关于的不等式；

    （2）若函数的图象恒在函数图象的上方，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    为了解少年儿童的肥胖是否与常喝碳酸饮料有关，现对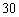名小学六年级学生进行了问卷调查，并得到如下列联表．平均每天喝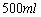以上为“常喝”，体重超过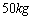为“肥胖”．

    常喝

    不常喝

    合计

    肥胖

    2

    不肥胖

    18

    合计

    30

    已知在全部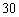人中随机抽取1人，抽到肥胖的学生的概率为．

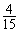    （1）请将上面的列联表补充完整；

    （2）是否有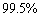的把握认为肥胖与常喝碳酸饮料有关？请说明你的理由；

    （3）已知常喝碳酸饮料且肥胖的学生中恰有2名女生，现从常喝碳酸饮料且肥胖的学生中随机抽取2人参加一个有关健康饮食的电视节目，求恰好抽到一名男生和一名女生的概率．

    参考数据：

    0．150

    0．100

    0．050

    0．025

    0．010

    0．005

    0．001

    2．072

    2．706

    3．841

    5．024

    6．635

    7．879

    10．828

    查看答案和解析>>

    同步练习册答案