
分析 (Ⅰ)作差法化简1-2(2ab+bc+ca+$\frac{{c}^{2}}{2}$)=(a+b+c)2-(4ab+2bc+2ca+c2),从而证明;
(Ⅱ)易知$\frac{{a}^{2}}{b}$+b≥2a,$\frac{{c}^{2}}{b}$+b≥2c,$\frac{{b}^{2}}{c}$+c≥2b,$\frac{{a}^{2}}{c}$+c≥2a,$\frac{{c}^{2}}{a}$+a≥2c,$\frac{{b}^{2}}{a}$+a≥2b;从而证明.
解答 证明:(Ⅰ)∵1-2(2ab+bc+ca+$\frac{{c}^{2}}{2}$)
=(a+b+c)2-(4ab+2bc+2ca+c2)
=a2+b2-2ab=(a-b)2≥0,
∴2(2ab+bc+ca+$\frac{{c}^{2}}{2}$)≤1,
∴2ab+bc+ca+$\frac{{c}^{2}}{2}$$≤\frac{1}{2}$;
(Ⅱ)∵$\frac{{a}^{2}}{b}$+b≥2a,$\frac{{c}^{2}}{b}$+b≥2c,$\frac{{b}^{2}}{c}$+c≥2b,$\frac{{a}^{2}}{c}$+c≥2a,$\frac{{c}^{2}}{a}$+a≥2c,$\frac{{b}^{2}}{a}$+a≥2b;
∴$\frac{{a}^{2}}{b}$+b+$\frac{{c}^{2}}{b}$+b+$\frac{{b}^{2}}{c}$+c+$\frac{{a}^{2}}{c}$+c+$\frac{{c}^{2}}{a}$+a+$\frac{{b}^{2}}{a}$+a≥4(a+b+c),
即$\frac{{a}^{2}+{c}^{2}}{b}$+$\frac{{b}^{2}+{c}^{2}}{a}$+$\frac{{a}^{2}+{b}^{2}}{c}$+2(a+b+c)≥4(a+b+c),
故$\frac{{a}^{2}+{c}^{2}}{b}$+$\frac{{b}^{2}+{c}^{2}}{a}$+$\frac{{a}^{2}+{b}^{2}}{c}$≥2.
点评 本题考查不等式的证明方法的应用,应用了作差法.


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{3}$,$\frac{1}{5}$] | B. | [-$\frac{1}{3}$,1] | C. | (-∞,-$\frac{1}{3}$]∪[$\frac{1}{5}$,+∞) | D. | (-∞,-$\frac{1}{3}$]∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:选择题
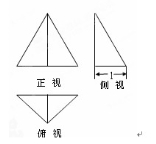
已知某个三棱锥的三视图如图所示,其中正视图是等边三角形,侧视图是直角三角形,俯视图是等腰直角三角形,则此三棱锥的体积等于( )
A.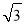 B.
B.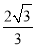 C.
C.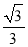 D.
D.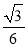
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 报名参加学科竞赛 | 未报名参加学科竞赛 | |
| 报名参加自主招生 | 2 | 4 |
| 未报名参加自主招生 | 6 | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com