
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
分析 由$\frac{2z+m}{z-3}=i$,得z=$\frac{m+3i}{-2+i}$,再由复数代数形式的乘除运算化简复数z,又z的实部与虚部之和为0,列出等式求解m即可得答案.
解答 解:由$\frac{2z+m}{z-3}=i$,
得$z=\frac{m+3i}{-2+i}=\frac{(m+3i)(-2-i)}{(-2+i)(-2-i)}$=$\frac{-2m+3-(6+m)i}{5}=\frac{-2m+3}{5}-\frac{6+m}{5}i$,
又z的实部与虚部之和为0,
则$\frac{-2m+3}{5}-\frac{6+m}{5}=0$,
解得m=-1.
故选:B.
点评 本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
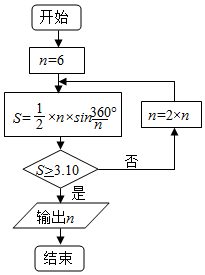 公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为( )
公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为( )| A. | 12 | B. | 24 | C. | 36 | D. | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知p,m>0,抛物线E:x2=2py上一点M(m,2)到抛物线焦点F的距离为$\frac{5}{2}$.
已知p,m>0,抛物线E:x2=2py上一点M(m,2)到抛物线焦点F的距离为$\frac{5}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com