
| A. | [0,+∞) | B. | (2,+∞) | C. | (2,8) | D. | (8,+∞) |
分析 B,O,C三点不可能在同一直线上,从而$\overrightarrow{OC}•\overrightarrow{OB}$=cos∠BOC∈(-1,1),推导出${λ}^{2}=1+{μ}^{2}-2μ\overrightarrow{OC}•\overrightarrow{OB}$,记f(μ)=λ2+(μ-3)2.则f(μ)=2${μ}^{2}-6μ-2μ\overrightarrow{OC}•\overrightarrow{OB}+10$,由此能求出λ2+(?-3)2的取值范围.
解答 解:∵A,B,C是圆x2+y2=1上相异三点,∴依题意B,O,C三点不可能在同一直线上,
∴$\overrightarrow{OC}•\overrightarrow{OB}$=|$\overrightarrow{OC}$|•|$\overrightarrow{OB}$|cos∠BOC=cos∠BOC∈(-1,1),
又∵存在正实数λ,? 使得 $\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$,∴$λ\overrightarrow{OA}=\overrightarrow{OC}-μ\overrightarrow{OB}$,
∴${λ}^{2}=1+{μ}^{2}-2μ\overrightarrow{OC}•\overrightarrow{OB}$,
记f(μ)=λ2+(μ-3)2.
则f(μ)=1+μ2-2$μ\overrightarrow{OC}•\overrightarrow{OB}$+(μ-3)2=2${μ}^{2}-6μ-2μ\overrightarrow{OC}•\overrightarrow{OB}+10$,
∴f(μ)>2μ2-8μ+10=2(μ-2)2+2≥2,且f(μ)<2μ2-4μ+10=2(μ-1)2+8 无最大值,
故λ2+(?-3)2的取值范围是(2,+∞).
点评 本题考查代数式的取值范围的求法,是中档题,解题时要认真审题,注意圆的方程、直线方程、向量的数量积的性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | (-2,+∞) | B. | (3,+∞) | C. | (-∞,-2) | D. | (-∞,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
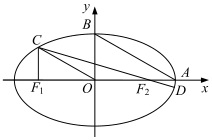 如图,在平面直角坐标系xOy中,设椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.
如图,在平面直角坐标系xOy中,设椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | (-∞,2] | C. | (2,+∞) | D. | (-∞,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com