
分析 (Ⅰ)结合已知新定义即可写出符合条件的数列;
(Ⅱ)设该21阶“期待数列”的公差为d,由题意可得,a1+a2+a3+…+a21=0,结合等差数列的求和公式可求a1+a21=0,从而可求得a11=0,进而可得a12=d,可求通项公式;
(Ⅲ)当k=n时,显然:|Sn|=0$≤\frac{1}{2}$成立; 当k<n时,根据条件①得Sk=a1+a2+…+ak=-(ak+1+ak+2+…+an),从而可求|Sk|,再利用不等式的性质即可证明.
解答 解:(Ⅰ)数列-$\frac{1}{2}$,0,$\frac{1}{2}$为三阶期待数列…(1分)
数列-$\frac{3}{8}$,-$\frac{1}{8}$,$\frac{1}{8}$,$\frac{3}{8}$为四阶期待数列,…(3分)
(Ⅱ)设该21阶“期待数列”的公差为d,
因为a1+a2+a3+…+a21=0,
∴a1+a21=0,
即a11=0,
∴a12=d,…(5分)
当d>0时,据期待数列的条件①②可得a12+a13+…+a21=$\frac{1}{2}$
∴10d+45d=$\frac{1}{2}$,∴d=$\frac{1}{110}$(6分)
∴该数列的通项公式为an=a11+(n-11)d=$\frac{n-11}{110}$(n∈N*且n≤2013).…(8分)
(Ⅲ)当k=n时,显然:|Sn|=0$≤\frac{1}{2}$成立; …(9分)
当k<n时,根据条件①得Sk=a1+a2+…+ak=-(ak+1+ak+2+…+an),…(10分)
即|Sk|=|a1+a2+…+ak|=|ak+1+ak+2+…+an|,…(11分)
∴2|Sk|=|a1+a2+…+ak|+|ak+1+ak+2+…+an|=1
∴|Sk|≤$\frac{1}{2}$(14分)
点评 本题以新定义为载体主要考查了数列的通项及求和公式的应用,解答本题的关键是具备一定的逻辑推理的运算的能力


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | (2,+∞) | C. | (2,8) | D. | (8,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-32) | B. | (-∞,-27) | C. | (-32,-27) | D. | (-32,-27] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
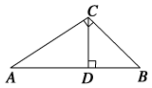
| A. | $\frac{3}{2}$ | B. | $\frac{9}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com