
| A. | λ≤3 | B. | λ≤4 | C. | 2≤λ≤3 | D. | 3≤λ≤4 |
分析 不等式nlog2(Tn+4)-λbn+7≥3n化为n2-n+7≥λ(n+1),可得λ≤$\frac{{n}^{2}-n+7}{n+1}$对一切n∈N*恒成立,利用不等式,即可得出结论.
解答 解∵an=2n+1,
∴Tn=$\frac{4(1-{2}^{n})}{1-2}$=2n+2-4.
不等式nlog2(Tn+4)-λ(n+1)+7≥3n化为n2-n+7≥λ(n+1),
∵n∈N*,
∴λ≤$\frac{{n}^{2}-n+7}{n+1}$对一切n∈N*恒成立.
而$\frac{{n}^{2}-n+7}{n+1}$=$\frac{(n+1)^{2}-3(n+1)+9}{n+1}$=(n+1)+$\frac{9}{n+1}$-3≥2$\sqrt{(n+1)•\frac{9}{n+1}}$-3=3,
当且仅当n+1=$\frac{9}{n+1}$即n=2时等号成立,
∴λ≤3,
故选:A.
点评 本题考查数列的通项于求和,突出考查基本不等式的运用,考查运算、分析、求解的能力,属于中档题.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:选择题
| A. | a,b,c均不为0 | B. | a,b,c中至多有一个为0 | ||
| C. | a,b,c中至少有一个为0 | D. | a,b,c中至少有一个不为0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3} | B. | {2,3,4} | C. | {0,1,2,3} | D. | {0,2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A${\;}_{4}^{3}$ | B. | C${\;}_{4}^{3}$ | C. | 34 | D. | 43 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{4}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{a-b}{c}$>0 | B. | ac2>bc2 | C. | (a+b)( $\frac{1}{a}$+$\frac{1}{b}$)>4 | D. | a2+b2+2>2a+2b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3+2\sqrt{2}}}{4}$ | B. | $2\sqrt{2}$ | C. | $\frac{{2+2\sqrt{2}}}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 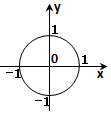 | B. | 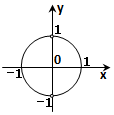 | C. | 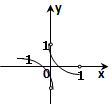 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com