
分析 (1)由已知得到数列{an}的前n项和,再由n≥2时,an=Sn-Sn-1求得数列通项公式,验证首项后得答案;再由b1=a1,b2=a4求出数列{bn}的首项和公比,进一步得到数列{bn}的通项公式;
(2)把数列{an}、{bn}的通项公式代入${c_n}={({-1})^n}{a_n}+{b_n}$,利用数列的分组求和求得数列{cn}的前n项和Tn.
解答 解:(1)由已知,${S}_{n}={n}^{2}+2n$.
当n≥2时,${a}_{n}={S}_{n}-{S}_{n-1}=({n}^{2}+2n)-[(n-1)^{2}+2(n-1)]$=2n+1.
当n=1时,a1=3适合上式.
∴an=2n+1;
由于b1=a1=3,b2=a4=9,
∴等比数列{bn}的公比为3,
∴${b}_{n}={3}^{n}$;
(2)${c_n}={({-1})^n}{a_n}+{b_n}$,
当n为偶数时,Tn=[(-3+5)+(-7+9)+…-(2n-1)+(2n+1)]+(3+32+…+3n)
$2×\frac{n}{2}+\frac{3(1-{3}^{n})}{1-3}=\frac{{3}^{n+1}}{2}+n-\frac{3}{2}$;
当n为奇数时,n-1为偶数,
${T}_{n}={T}_{n-1}+{c}_{n}=[\frac{{3}^{(n-1)+1}}{2}+(n-1)-\frac{3}{2}]+$$(-1)×(2n+1)+{3}^{n}=\frac{{3}^{n+1}}{2}-n-\frac{7}{2}$.
综上所述,${T}_{n}=\left\{\begin{array}{l}{\frac{{3}^{n+1}}{2}+n-\frac{3}{2},n为偶数}\\{\frac{{3}^{n+1}}{2}-n-\frac{7}{2},n为奇数}\end{array}\right.$
点评 本题考查数列递推式,考查了数列的分组求和,属中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
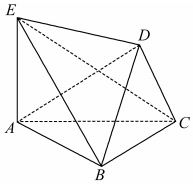 如图,六面体ABCDE中,面DBC⊥面ABC,AE⊥面ABC.
如图,六面体ABCDE中,面DBC⊥面ABC,AE⊥面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [6,8] | B. | [-2,6] | C. | [0,2] | D. | [6,10] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{25}{4}$ | B. | $\frac{7}{4}$ | C. | -$\frac{9}{4}$ | D. | $\frac{41}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
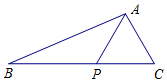 如图,在△ABC中,点P在BC边上,∠PAC=60°,PC=2,AP+AC=4.
如图,在△ABC中,点P在BC边上,∠PAC=60°,PC=2,AP+AC=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com