考点:命题的真假判断与应用
专题:空间向量及应用
分析:结合平行六面体的性质,可判断①,运用空间向量的加减运算,解决②,注意重心的性质的运用,④可由①的分析得到;③通过面面平行的判定和性质可得;⑤可由向量的模求得.
解答:
解:①连接A
1C
1,AC,A
1C,A
1E,由平行六面体的性质得:四边形A
1ACC
1是平行四边形,对角线互相平分且交于点O,延长A
1E交AC于H,且H为AC的中点,则E为三角形A
1AC的重心,有AE=2OE,同理C
1F=2OF,
所以点E,F为线段AC
1的两个三等分点,故①对;
②∵
=-=-=
-(+)=
---=
+-,故②错;
③再取A
1B
1的中点K,连接KM,KN,由面面平行的判定定理可得:面KMN∥面A
1BD,所以直线MN∥面A
1BD,
所以直线MN与面A
1DB没有交点,故③错;
④由①得A
1E=2EH,所以E为△A
1BD的重心,故④错;
⑤因为∠A
1AD=∠A
1AB=∠BAD=60°,且AA
1=AB=AD=1,所以三角形A
1BD为等边三角形,即
三棱锥A
1-ABD为正三棱锥,∵
=++,|
|==
=,故⑤对.
故答案为:①⑤
点评:本题考查平行六面体的性质,空间向量的加法、减法和数量积、模的概念,考查运算能力,是一道中档题.

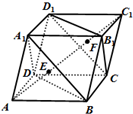 已知平行六面体ABCD-A1B1C1D1,AC1与平面A1BD,CB1D1交于E,F两点.给出以下命题,其中真命题有
已知平行六面体ABCD-A1B1C1D1,AC1与平面A1BD,CB1D1交于E,F两点.给出以下命题,其中真命题有

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案