
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 在①中,当z=0时,‖z‖=0;反之,当‖z‖=0时,z=0;在②中,z=a+bi,$\overline{z}$=a-bi,从而‖z‖=‖$\overline{z}$‖=|a|+|b|;在③中,当z1=2+3i,z2=3+2i时,不成立;④由绝对值的性质得到‖z1-z3‖≤‖z1-z2‖+‖z2-z3‖恒成立.
解答 解:由复数z=a+bi(a、b∈R,i为虚数单位),定义‖z‖=|a|+|b|,知:
在①中,对任何复数,都有‖z‖≥0,
当z=0时,‖z‖=0;反之,当‖z‖=0时,z=0,
∴等号成立的充要条件是z=0,故①成立;
在②中,∵z=a+bi,$\overline{z}$=a-bi,∴‖z‖=‖$\overline{z}$‖=|a|+|b|,故②成立;
在③中,当z1=2+3i,z2=3+2i时,‖z1‖=‖z2‖,但z1≠±z2,故③错误;
④对任何复数z1,z2,z3,
设z1=a1+b1i,z2=a2+b2i,z3=a3+b3i,
则‖z1-z3‖=|a1-a3|+|b1-b3|,
‖z1-z2‖+‖z2-z3‖=|a1-a2|+|a2-a3|+|b1-b2|+|b2-b3|,
|a1-a3|≤|a1-a2|+|a2-a3|,
|b1-b3|≤|b1-b2|+|b2-b3|,
∴‖z1-z3‖≤‖z1-z2‖+‖z2-z3‖恒成立.故④成立.
故选:C.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意绝对值性质、复数概念及性质的合理运用.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{39}{79}$ | B. | $\frac{1}{80}$ | C. | $\frac{1}{2}$ | D. | $\frac{41}{80}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
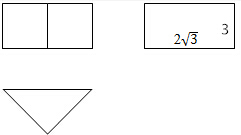 若一个三棱柱ABC-A1B1C1的三视图如图所示,主视图与左视图均为矩形,俯视图为一个正三角形.
若一个三棱柱ABC-A1B1C1的三视图如图所示,主视图与左视图均为矩形,俯视图为一个正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com