Question

5．随机取两个正实数x，y，满足x+y＜2，则y＞x²的概率是$\frac{7}{12}$．

Answer 1

分析 首先由题意，画出示意图，利用满足条件的区域面积求概率．

解答 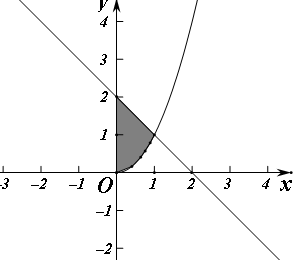解：由题意随机取两个正实数x，y，满足x+y＜2，对应区域面积为$\frac{1}{2}×2×2$=2，满足y＞x²的区域如图阴影部分，
面积为${∫}_{0}^{1}（2-x-{x}^{2}）dx$=（2x-$\frac{1}{2}$x²-$\frac{1}{3}$x³）|${\;}_{0}^{1}$=$\frac{7}{6}$，
所以所求概率是$\frac{\frac{7}{6}}{2}=\frac{7}{12}$；
故答案为：$\frac{7}{12}$．

点评 本题考查了几何概型的概率求法；关键是明确几何测度为区域面积，利用面积比求概率．