Question

【题目】近年来，在新高考改革中，打破文理分科的“”模式初露端倪，其中语、数、外三门课为必考科目，剩下三门为选考科目选考科目成绩采用“赋分制”，即原始分数不直接用，而是按照学生分数在本科目考试的排名来划分等级并以此打分得到最后得分，假定省规定：选考科目按考生成绩从高到低排列，按照占总体、、、分别赋分分、分、分、分，为了让学生们体验“赋分制”计算成绩的方法，省某高中高一（）班（共人）举行了以此摸底考试（选考科目全考，单料全班排名），知这次摸底考试中的物理成绩（满分分）频率分布直方图，化学成绩（满分分）茎叶图如图所示，小明同学在这次考试中物理分，化学多分．

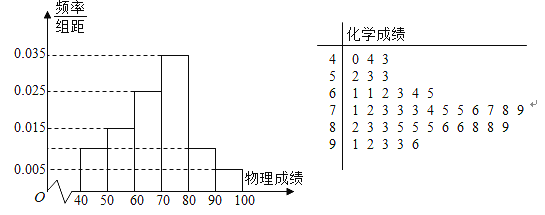
（1）采用赋分制后，求小明物理成绩的最后得分；

（2）若小明的化学成绩最后得分为分，求小明的原始成绩的可能值；

（3）若小明必选物理，其他两科从化学、生物、历史、地理、政治五科中任选，求小明此次考试选考科目包括化学的概率．

Answer 1

【答案】（1）分；（2）；（3）.

【解析】

（1）根据物理分判断所处的百分比，根据百分比确定分数；（2）先排除赋分分的分数，然后利用百分比计算赋分分的人数，结合数据，给出可能的取值；（3）采用列举法以及古典概型的概率计算公式来求解.

（1）∵，，

∴此次考试物理成绩落在，内的频率依次为，，频率之和为，且小明的物理成绩为分，大于分，处于前，

∴小明物理成绩的最后得分为分.

（2）因为名学生中，赋分分的有人，这六人成绩分别为，，，，，；赋分分的有人，其中包含多分的共人，多分的有人，分数分别为，，，；因为小明的化学成绩最后得分为分，且小明化学多分，所以小明的原始成绩的可能值为，，，.

（3）记物理、化学、生物、历史、地理、政治依次为，，，，，，小明的所有可能选法有，，，，，

，，，，共10种，

其中包括化学的有，，，共4种，

∵若小明必选物理，其他两科在剩下的五科中任选，所选科目包括化学的概率为：.