
分析 (1)设椭圆C:$\frac{{x}^{2}}{4{m}^{2}}+\frac{{y}^{2}}{2{m}^{2}}$=1,M(x1,y1),N(x2,y2),利用点差法能求出直线MN的方程.
(2)设F1(c,0),则$\overrightarrow{{F}_{1}M}$=(x1-c,y1),$\overrightarrow{{F}_{1}N}$=(x2-c,y2),从而得到3c2-12c+1+3(x1x2+y1y2)=0,联立联立$\left\{\begin{array}{l}{x+y-3=0}\\{{x}^{2}+2{y}^{2}=4{m}^{2}}\end{array}\right.$,得3x2-12x-4m2+18=0,从而x1x2+y1y2=9-$\frac{8{m}^{2}}{3}$,由此能求出椭圆C的方程.
解答 解:(1)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上的两点M,N,点P(2,1)为线段MN的中点,
椭圆的离心率为$\frac{\sqrt{2}}{2}$,
∴椭圆C:$\frac{{x}^{2}}{4{m}^{2}}+\frac{{y}^{2}}{2{m}^{2}}$=1,
设M(x1,y1),N(x2,y2),则x1+x2=4,y1+y2=2,
把M(x1,y1),N(x2,y2)代入椭圆C:$\frac{{x}^{2}}{4{m}^{2}}+\frac{{y}^{2}}{2{m}^{2}}$=1,
得$\left\{\begin{array}{l}{{{x}_{1}}^{2}+2{{y}_{1}}^{2}=4{m}^{2}}\\{{{x}_{2}}^{2}+2{{y}_{2}}^{2}=4{m}^{2}}\end{array}\right.$,∴(x1+x2)(x1-x2)+2(y1-y2)(y1+y2)=0,
∴4(x1-x2)+4(y1-y2)=0,∴k=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-1,
∴直线MN的方程为y-1=-(x-2),即x+y-3=0.
(2)设F1(c,0),则$\overrightarrow{{F}_{1}M}$=(x1-c,y1),$\overrightarrow{{F}_{1}N}$=(x2-c,y2),
∵$\overrightarrow{{F}_{1}M}$•$\overrightarrow{{F}_{1}N}$=-$\frac{1}{3}$,
∴(x1-c)(x2-c)+y1y2=-$\frac{1}{3}$,(*)
又x1+x2=4,故由(*)式整理,得:3c2-12c+1+3(x1x2+y1y2)=0,①
联立$\left\{\begin{array}{l}{x+y-3=0}\\{{x}^{2}+2{y}^{2}=4{m}^{2}}\end{array}\right.$,得3x2-12x-4m2+18=0,
△>0,x1+x2=4,x1x2=$\frac{18-4{m}^{2}}{3}$,
y1y2=(3-x1)(3-x2)=x1x2-3(x1+x2)+9,
∴x1x2+y1y2=2x1x2-3(x1+x2)+9=2×$\frac{18-4{m}^{2}}{3}$-3×4+9=9-$\frac{8{m}^{2}}{3}$,②
c=$\sqrt{4{m}^{2}-2{m}^{2}}$=$\sqrt{2}m$,③
①②③联立,得:2m2+12$\sqrt{2}m$-28=0,
解得m=$\sqrt{2}$或m=-7$\sqrt{2}$(舍),
∴椭圆C的方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$.
点评 本题考查直线方程的求法,考查椭圆方程的求法,是中档题,解题时要认真审题,注意点差数、椭圆性质的合理运用.


科目:高中数学 来源: 题型:选择题
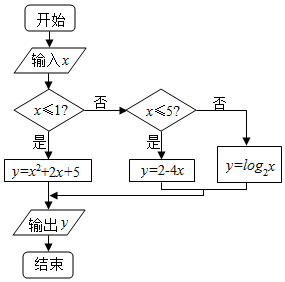
| A. | 2 | B. | ${log_2}\frac{π}{2}$ | C. | 2-2π | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
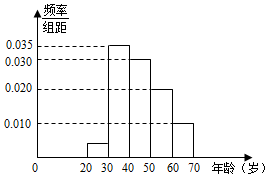 某市为庆祝北京夺得2022年冬奥会举办权,围绕“全民健身促健康,同心共筑中国梦”主题开展全民健身活动,组织方从参加活动的群众中随机抽取120名群众,按他们的年龄分组:第1组[20,30),第2组[30,40),第3组[40,50),第4组[50,60),第5组[60,70],得到的频率分布直方图如图所示.
某市为庆祝北京夺得2022年冬奥会举办权,围绕“全民健身促健康,同心共筑中国梦”主题开展全民健身活动,组织方从参加活动的群众中随机抽取120名群众,按他们的年龄分组:第1组[20,30),第2组[30,40),第3组[40,50),第4组[50,60),第5组[60,70],得到的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
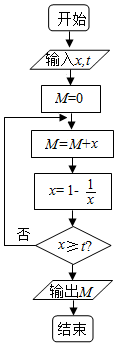
| A. | 3 | B. | $\frac{11}{3}$ | C. | $\frac{19}{6}$ | D. | $\frac{37}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n | B. | 2 | C. | 2n | D. | $\frac{n}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
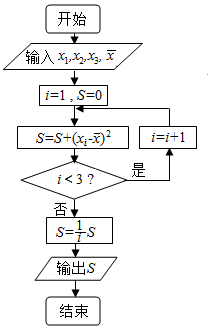
| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com