Question

3．在平面直角坐标系xOy中，A（4，0），B（2，4），C（0，2），动点M在△ABC区域内（含边界）运动，设$\overrightarrow{OM}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OC}$，则λ+μ的取值范围是[1，$\frac{5}{2}$]．

Answer 1

分析 作图并设M（x，y），从而由向量可得（x，y）=λ（4，0）+μ（0，2）；从而求得λ+μ=$\frac{x}{4}$+$\frac{y}{2}$，从而转化为线性规划问题求解即可．

解答 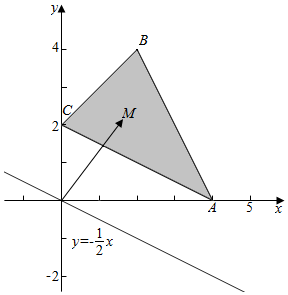解：如图，设M（x，y），
所以（x，y）=λ（4，0）+μ（0，2）；
故λ=$\frac{x}{4}$，μ=$\frac{y}{2}$，所以λ+μ=$\frac{x}{4}$+$\frac{y}{2}$，
问题等价于当M在△ABC内（含边界）运动时，
求z=$\frac{x}{4}$+$\frac{y}{2}$的取值范围，
运用线性规划知识可知
当M在点B时z_max=$\frac{5}{2}$，当M在AC上任意一点时z_min=1，
所以λ+μ取值范围是[1，$\frac{5}{2}$]．
故答案为：[1，$\frac{5}{2}$]．

点评 本题考查了线性规划的变形应用及平面向量的应用，同时考查了数形结合的思想方法应用，属于中档题．