Question

14．如图所示，在多面体A₁B₁D₁-ABCD，四边形AA₁B₁B，ADD₁A₁，ABCD均为正方形，E为B₁D₁的中点，过A₁，D，E的平面交CD₁于F
（Ⅰ）证明：EF∥B₁C；
（Ⅱ）求二面角E-A₁D-B₁的正切值；
（Ⅲ）求直线A₁C与平面B₁CD₁所成角的余弦值．

Answer 1

分析 （Ⅰ）由线面平行的判定定理证明：B₁C∥A₁DEF，即可证明EF∥B₁C；
（Ⅱ）将多面体A₁B₁D₁-ABCD补成正方体A₁B₁C₁D₁-ABCD，取B₁C的中点G，A₁D的中点H，连接C₁G，GH，C₁H，则∠C₁HG是二面角C₁-A₁D-B₁的平面角，即可求二面角E-A₁D-B₁的正切值；
（Ⅲ）连接EC，A₁C，证明∠A₁CE是直线A₁C与平面B₁CD₁所成的角，利用余弦定理即可求直线A₁C与平面B₁CD₁所成角的余弦值．

解答 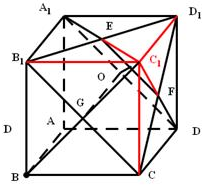（Ⅰ）证明：∵B₁C∥A₁D，B₁C?平面A₁DEF，A₁D?平面A₁DEF
由线面平行的判定定理有B₁C∥A₁DEF
又过B₁C的平面B₁CD₁与平面A₁DEF相交于EF，
由线面平行的性质定理有B₁C∥EF
（Ⅱ）解：将多面体A₁B₁D₁-ABCD补成正方体A₁B₁C₁D₁-ABCD
如图，并设棱长为a，∴二面角E-A₁D-B₁即为C₁-A₁D-B₁
取B₁C的中点G，A₁D的中点H，连接C₁G，GH，C₁H
可知C₁G⊥平面A₁B₁CD，∵GH⊥A₁D，∴C₁H⊥A₁D，
故∠C₁HG是二面角C₁-A₁D-B₁的平面角，
在RT△C₁HG中，${C_1}G=\frac{{\sqrt{2}}}{2}a，GH=a$，∴$tan∠{C_1}HG=\frac{{{C_1}G}}{GH}=\frac{{\sqrt{2}}}{2}$
则二面角E-A₁D-B₁的正切值为$\frac{{\sqrt{2}}}{2}$．
（Ⅲ）解：连接EC，A₁C
∵B₁D₁⊥平面AA₁C₁C，∴平面B₁CD₁⊥平面AA₁C₁C．∴EC是A₁C在平面B₁CD₁上的射影，
故∠A₁CE是直线A₁C与平面B₁CD₁所成的角，
在△C₁AE中，${A_1}C=\sqrt{3}a，{A_1}E=\frac{{\sqrt{2}}}{2}a，EC=\frac{{\sqrt{6}}}{2}a$，
∴$cos∠{A_1}CE=\frac{{{{（\sqrt{3}a）}^2}+{{（\frac{{\sqrt{6}}}{2}a）}^2}-{{（\frac{{\sqrt{2}}}{2}a）}^2}}}{{2•\sqrt{3}a•\frac{{\sqrt{6}}}{2}a}}=\frac{{2\sqrt{2}}}{3}$
则直线A₁C与平面B₁CD₁所成角的余弦值为$\frac{{2\sqrt{2}}}{3}$．

点评 本题考查线面平行的判定与性质，考查线面角、二面角，考查学生分析解决问题的能力，考查学生的计算能力，属于中档题．