
分析 (1)求解指数不等式化简集合A,结合x∈N*得到集合A中的元素,则A的子集的个数可求;
(2)对集合B分类讨论,当B为空集时满足题意,求出m的范围,当B≠∅时,由两集合端点值间的关系列不等式求解.
解答 解:(1)A={x|$\frac{1}{32}$≤$\frac{1}{{2}^{x}}$≤4}={x|-2≤x≤5},
∵x∈N*,∴A={1,2,3,4,5}.
则A的子集的个数为25=32;
(2)若m-1>2m+1,即m<-2时,B=∅,
此时且A∩B=∅;
当B≠∅时,要使A∩B=∅,
则5<m-1或2m+1<-2.
解得:m>6或m$<-\frac{3}{2}$.
点评 本题考查子集与真子集,考查了集合的包含关系及其应用,训练了指数不等式的解法,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
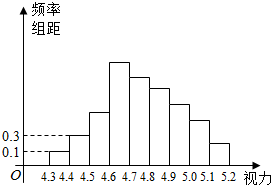 为了解某校学生的视力情况,随机抽查了该校的100名学生,得到如图所示的频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频数和为40,后6组的频数和为87,设最大频率a视力在4.5到5.2之间的学生数b,则a,b的值分别为( )
为了解某校学生的视力情况,随机抽查了该校的100名学生,得到如图所示的频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频数和为40,后6组的频数和为87,设最大频率a视力在4.5到5.2之间的学生数b,则a,b的值分别为( )| A. | 0.27,96 | B. | 0.27,83 | C. | 2.7,78 | D. | 2.7,83 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1007 | B. | 1008 | C. | 2014 | D. | 2015 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com