
分析 (1)设公差d不等于零的等差数列{an},运用等差数列的通项公式和求和公式,解方程可得首项和公差,即可得到所求;
(2)求得$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),运用数列的求和方法:裂项相消求和,可得Tn,再由参数分离和数列的单调性,即可得到所求范围,可得最小值.
解答 解:(1)设公差d不等于零的等差数列{an},
an=a1+(n-1)d,Sn=na1+$\frac{n(n-1)}{2}$d,
由S3=9,可得3a1+3d=9,即为a1+d=3,
a1.a2.a5成等比数列,可得a1a5=a22,
即为a1(a1+4d)=(a1+d)2,
解得a1=1,d=2(0舍去)
即有an=2n-1;
(2)$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),
Tn=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)=$\frac{1}{2}$(1-$\frac{1}{2n+1}$)=$\frac{n}{2n+1}$,
由题意可得$\frac{n}{2n+1}$≤λ(2n+1),即为
λ≥$\frac{n}{(2n+1)^{2}}$=$\frac{1}{4n+\frac{1}{n}+4}$,
由4n+$\frac{1}{n}$在[1,+∞)递增,可得最小值为4+1=5,
由Tn≤λan+1对 一切n∈N*恒成立,
可得λ≥$\frac{1}{5+4}$=$\frac{1}{9}$.
即有实数λ的最小值为$\frac{1}{9}$.
点评 本题考查等差数列的通项公式和求和公式的运用,考查等比数列的中项的性质,同时考查不等式恒成立问题的解法,注意运用参数分离和数列的单调性求最值,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知:⊙O的方程为x2+y2=9,点A(5,0),过点A作⊙O的切线AP,P为切点.
已知:⊙O的方程为x2+y2=9,点A(5,0),过点A作⊙O的切线AP,P为切点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
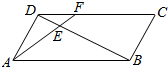 如图,点E是平行四边形ABCD对角线BD的n(n∈N且n≥2)等分点中最靠近点D的那点.线段AE的延长线交CD于点F,若向量$\overrightarrow{AF}=\frac{1}{n-1}\overrightarrow{AB}+x\overrightarrow{AD}$,则实数x的值为1.
如图,点E是平行四边形ABCD对角线BD的n(n∈N且n≥2)等分点中最靠近点D的那点.线段AE的延长线交CD于点F,若向量$\overrightarrow{AF}=\frac{1}{n-1}\overrightarrow{AB}+x\overrightarrow{AD}$,则实数x的值为1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com