
分析 确定S△ABC=$\frac{3\sqrt{3}}{4}$,△ABC的外接圆的半径为$\sqrt{3}$,利用三棱锥D-ABC的体积的最大值为$\frac{3\sqrt{3}}{4}$,可得D到平面ABC的最大距离为1,再利用射影定理,即可求出球的半径,即可求出球O的表面积.
解答 解:∵AB=BC=$\sqrt{3}$,AC=3,
∴S△ABC=$\frac{1}{2}$×3×$\sqrt{3-\frac{9}{4}}$=$\frac{3\sqrt{3}}{4}$,
∵三棱锥D-ABC的体积的最大值为$\frac{3\sqrt{3}}{4}$,
∴D到平面ABC的最大距离为1,
∵cos∠A=$\frac{\sqrt{3}}{2}$,
∴sin∠A=$\frac{1}{2}$,
设△ABC的外接圆的半径为r,则2r=2$\sqrt{3}$,∴r=$\sqrt{3}$;
设球的半径为R,则($\sqrt{3}$)2=1×(2R-1),
∴R=2,
∴球O的表面积为4πR2=16π.
故答案为:16π.
点评 本题考查球的半径,考查体积的计算,确定D到平面ABC的最大距离为1是关键.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
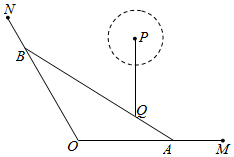 如图,A、B是海岸线OM、ON上的两个码头,Q为海中一小岛,在水上旅游线AB上,测得tan∠MON=-3,OA=6km,Q到海岸线OM、ON的距离分别为2km,$\frac{7\sqrt{10}}{5}$km.
如图,A、B是海岸线OM、ON上的两个码头,Q为海中一小岛,在水上旅游线AB上,测得tan∠MON=-3,OA=6km,Q到海岸线OM、ON的距离分别为2km,$\frac{7\sqrt{10}}{5}$km.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=lnex与y=elnx | B. | $y={t^{\frac{1}{2}}}$与$y={t^{\frac{2}{4}}}$ | ||
| C. | y=x0与y=$\frac{1}{x^0}$ | D. | $y=cos(t+\frac{π}{2})$与y=sint |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com