练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．求函数y=$\frac{sinx}{2+cosx}$的最大值．

    分析 变形可得y=$\frac{sinx}{2+cosx}$=$\frac{sinx-0}{cosx-（-2）}$表示点（cosx，sinx）和A（-2，0）连线的斜率，由直线和圆的知识可得．

    解答 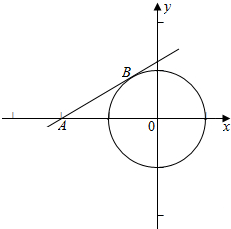解：y=$\frac{sinx}{2+cosx}$=$\frac{sinx-0}{cosx-（-2）}$，表示点（cosx，sinx）和A（-2，0）连线的斜率，
    而由cos2x+sin2x=1可知点（cosx，sinx）在单位圆x2+y2=1上，
    数形结合可得在图中切线AB时，y取最大值，
    由三角形的知识可得∠BAO=30°，
    故y取最大值tan30°=$\frac{\sqrt{3}}{3}$．

    点评 本题考查三角函数的最值，数形结合是解决问题的关键，属中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    2．若等轴双曲线经过点M（1，2），则此双曲线的半焦距为$\sqrt{6}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

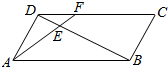    3．如图，点E是平行四边形ABCD对角线BD的n（n∈N且n≥2）等分点中最靠近点D的那点．线段AE的延长线交CD于点F，若向量$\overrightarrow{AF}=\frac{1}{n-1}\overrightarrow{AB}+x\overrightarrow{AD}$，则实数x的值为1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．已知点A，B，C，D均在球O上，AB=BC=$\sqrt{3}$，AC=3，若三棱锥D-ABC体积的最大值为$\frac{3\sqrt{3}}{4}$，则球O的表面积为16π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．设数列{an}的首项a1=1，且2an+1=an+$\frac{1-n}{n（n+1）}$，则an=${2}^{2-n}-\frac{1}{n}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知tanα=$\frac{3}{4}$，cos（β-α）=-$\frac{\sqrt{2}}{10}$
    （1）求sin2α-sinαcosα的值．
    （2）若0＜α＜$\frac{π}{2}$＜β＜π，求β的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．直线a与平面α所成的角为50°，直线b∥α，则b与α所成的角等于（　　）
    A．40°B．50°C．90°D．150°

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．求曲线C1：y=$\frac{1}{x}$与曲线C2：y═-x2的公切线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．若函数$f（x）=1-\sqrt{x}$，$g（x）=\sqrt{1-x}+\sqrt{x}$，则f（x）+g（x）=1$+\sqrt{1-x}$（0≤x≤1）．

    查看答案和解析>>

    同步练习册答案