
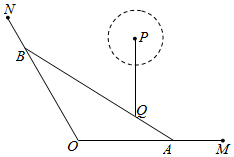
 如图,A、B是海岸线OM、ON上的两个码头,Q为海中一小岛,在水上旅游线AB上,测得tan∠MON=-3,OA=6km,Q到海岸线OM、ON的距离分别为2km,$\frac{7\sqrt{10}}{5}$km.
如图,A、B是海岸线OM、ON上的两个码头,Q为海中一小岛,在水上旅游线AB上,测得tan∠MON=-3,OA=6km,Q到海岸线OM、ON的距离分别为2km,$\frac{7\sqrt{10}}{5}$km.分析 (1)利用△AOB的面积列出等式求出OB,然后使用余弦定理求出AB;
(2)求出AP,∠PAQ,假设航行t小时候到达D点,使用余弦定理求出PD,比较PD与r的大小关系即可判断强水波是否波及航行.
解答 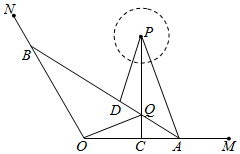 解:(1)连结OQ,则S△OAQ=$\frac{1}{2}×OA×$2=6,S△OBQ=$\frac{1}{2}×OB×$$\frac{7\sqrt{10}}{5}$=$\frac{7\sqrt{10}}{10}$OB.
解:(1)连结OQ,则S△OAQ=$\frac{1}{2}×OA×$2=6,S△OBQ=$\frac{1}{2}×OB×$$\frac{7\sqrt{10}}{5}$=$\frac{7\sqrt{10}}{10}$OB.
∵tan∠MON=-3,∴sin∠MON=$\frac{3\sqrt{10}}{10}$.cos∠MON=-$\frac{\sqrt{10}}{10}$,∴S△AOB=$\frac{1}{2}×OA×OB×sin∠MON$=$\frac{9\sqrt{10}}{10}$OB.
∴6+$\frac{7\sqrt{10}}{10}$OB=$\frac{9\sqrt{10}}{10}$OB.∴OB=3
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}-2OA•OBcos∠MON}$=$\sqrt{162}$=9$\sqrt{2}$.
(2)在△ABO中,由正弦定理得$\frac{OB}{sinA}=\frac{AB}{sin∠MON}$,即$\frac{3\sqrt{10}}{sinA}=\frac{9\sqrt{2}}{\frac{3\sqrt{10}}{10}}$,∴sinA=$\frac{\sqrt{2}}{2}$.
延长PQ交OA于C,连结AP,则QC=2,AQ=2$\sqrt{2}$,cos∠AQP=-cos∠AQC=-sinA=-$\frac{\sqrt{2}}{2}$.∴sin∠AQP=$\frac{\sqrt{2}}{2}$.
∴AP=$\sqrt{A{Q}^{2}+P{Q}^{2}-2AQ•PQcos∠AQP}$=2$\sqrt{17}$.
∵$\frac{PQ}{sin∠PAQ}=\frac{AP}{sin∠AQP}$,∴sin∠PAQ=$\frac{3\sqrt{34}}{34}$.∴cos∠PAQ=$\frac{5\sqrt{34}}{34}$.
假设t小时候游轮航行到D处,连结PD,则0≤t$≤\frac{1}{2}$,AD=18$\sqrt{2}$t,
∴PD=$\sqrt{A{P}^{2}+A{D}^{2}-2AP•ADcos∠PAQ}$=$\sqrt{648{t}^{2}-360t+68}$.
令f(t)=PD2-r2=648t2-360t+68-216t3,则f′(t)=-648t2-1296t-360,
令f′(t)=0解得t=$\frac{1}{3}$或t=$\frac{5}{3}$(舍).
当$0≤t<\frac{1}{3}$时,f′(t)<0,当$\frac{1}{3}$<t$≤\frac{1}{2}$时,f′(t)>0,
∴fmin(t)=f($\frac{1}{3}$)=12>0.∴PD2-r2>0,即PD>r恒成立.
∴强水波不会波及游轮的航行.
点评 本题考查了正弦定理,余弦定理在解三角形中的应用,函数值的大小比较,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | y=|x| | B. | y=lnx | C. | y=x${\;}^{\frac{1}{3}}$ | D. | y=x-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
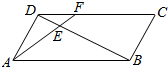 如图,点E是平行四边形ABCD对角线BD的n(n∈N且n≥2)等分点中最靠近点D的那点.线段AE的延长线交CD于点F,若向量$\overrightarrow{AF}=\frac{1}{n-1}\overrightarrow{AB}+x\overrightarrow{AD}$,则实数x的值为1.
如图,点E是平行四边形ABCD对角线BD的n(n∈N且n≥2)等分点中最靠近点D的那点.线段AE的延长线交CD于点F,若向量$\overrightarrow{AF}=\frac{1}{n-1}\overrightarrow{AB}+x\overrightarrow{AD}$,则实数x的值为1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>6 | B. | m>9 | C. | m>11 | D. | m>12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com