
| A. | m>6 | B. | m>9 | C. | m>11 | D. | m>12 |
分析 三角形的边长为正数,而且任意两边之和大于第三边才能构成三角形,故只需求出函数在区间$[{\frac{1}{3},3}]$上的最小值与最大值,从而可得不等式,即可求解.
解答 解:由f′(x)=3x2-3=3(x+1)(x-1)=0得到x1=1,x2=-1(舍去)
∵函数的定义域为$[{\frac{1}{3},3}]$,
∴函数在($\frac{1}{3}$,1)上f′(x)<0,(1,3)上f′(x)>0,
∴函数f(x)在区间($\frac{1}{3}$,1)单调递减,在区间(1,3)单调递增,
则f(x)min=f(1)=2m-2,f(3)=2m+18,f($\frac{1}{3}$)=2m-$\frac{26}{27}$,f(3)>f($\frac{1}{3}$),f(x)max=f(3)=2m+18
由题意知,f(1)=2m-2>0 ①;
f(1)+f(1)>f(3),即-4+4m>18+2m②
由①②得到m>11为所求.
故选:C.
点评 本题以函数为载体,考查构成三角形的条件,解题的关键是求出函数在区间[$\frac{1}{3}$,3]上的最小值与最大值,考查导数的综合应用.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:解答题
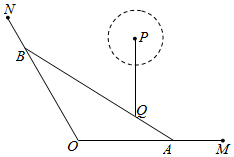 如图,A、B是海岸线OM、ON上的两个码头,Q为海中一小岛,在水上旅游线AB上,测得tan∠MON=-3,OA=6km,Q到海岸线OM、ON的距离分别为2km,$\frac{7\sqrt{10}}{5}$km.
如图,A、B是海岸线OM、ON上的两个码头,Q为海中一小岛,在水上旅游线AB上,测得tan∠MON=-3,OA=6km,Q到海岸线OM、ON的距离分别为2km,$\frac{7\sqrt{10}}{5}$km.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=lnex与y=elnx | B. | $y={t^{\frac{1}{2}}}$与$y={t^{\frac{2}{4}}}$ | ||
| C. | y=x0与y=$\frac{1}{x^0}$ | D. | $y=cos(t+\frac{π}{2})$与y=sint |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,e+1] | B. | [1,e] | C. | [0,1] | D. | [0,e] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 身高(单位:cm) | [180,185) | [185,190) | [190,195) | [195,200) | [200,205) | [205,210) |
| 人数 | 2 | 3 | 3 | 2 | 1 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 车型 概率 人 | A | B | C |
| 甲 | $\frac{1}{5}$ | p | q |
| 乙 | / | $\frac{2}{5}$ | $\frac{3}{5}$ |
| 车型 | A | B | C |
| 补贴金额(万元/辆) | 3 | 4 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com