
分析 (1)由题意可得函数为定义域为(-1,1)的奇函数,由f(-x)+f(x)=0可得a的方程,解方程可得a值;
(2)求反函数可得f-1(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$,代入解不等式可得.
解答 解:(1)由1+x>0和1-x>0可得-1<x<1,
∴函数f(x)=alog2(1+x)-log2(1-x)的定义域为(-1,1),
∵函数f(x)=alog2(1+x)-log2(1-x)图象关于原点对称,
∴函数f(x)为(-1,1)上的奇函数,
∴f(-x)+f(x)=0,即alog2(1-x)-log2(1+x)+alog2(1+x)-log2(1-x)=0,
故(a-1)[log2(1-x)-log2(1+x)]=(a-1)log2$\frac{1-x}{1+x}$=0,
∴a-1=0,解得a=1,故f(x)=log2(1+x)-log2(1-x)=log2$\frac{1+x}{1-x}$;
(2)由(1)可得y=log2$\frac{1+x}{1-x}$,∴$\frac{1+x}{1-x}$=2y,解得x=$\frac{{2}^{y}-1}{{2}^{y}+1}$,
∴f-1(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$,由f-1(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$>$\frac{1}{3}$可得3(2x-1)>2x+1,
化简可得2x>1,解得x>0,故不等式的解集为{x|x>0}
点评 本题考查对数函数的图象和性质,涉及反函数以指数函数的知识,属中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 已知:⊙O的方程为x2+y2=9,点A(5,0),过点A作⊙O的切线AP,P为切点.
已知:⊙O的方程为x2+y2=9,点A(5,0),过点A作⊙O的切线AP,P为切点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
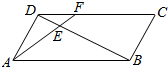 如图,点E是平行四边形ABCD对角线BD的n(n∈N且n≥2)等分点中最靠近点D的那点.线段AE的延长线交CD于点F,若向量$\overrightarrow{AF}=\frac{1}{n-1}\overrightarrow{AB}+x\overrightarrow{AD}$,则实数x的值为1.
如图,点E是平行四边形ABCD对角线BD的n(n∈N且n≥2)等分点中最靠近点D的那点.线段AE的延长线交CD于点F,若向量$\overrightarrow{AF}=\frac{1}{n-1}\overrightarrow{AB}+x\overrightarrow{AD}$,则实数x的值为1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com