
分析 (I)利用公式an=$\left\{\begin{array}{l}{{S}_{1},n=1}\\{{S}_{n}-{S}_{n-1},n≥2}\end{array}\right.$计算通项公式;
(II)先判断an的符号,得出数列{|an|}的前n项和与Sn的关系,再计算.
解答 解:(I)n=1时,a1=S1=2-3-10=-11,
当n≥2时,an=Sn-Sn-1=2n2-3n-10-[2(n-1)2-3(n-1)-10]=4n-5,
∴an=$\left\{\begin{array}{l}{-11,n=1}\\{4n-5,n≥2}\end{array}\right.$
(II)设数列{|an|}的前n项和为Tn,
由于n≥2时,an>0,n=1时,a1=-11<0,
故n=1时,Tn=|a1|=11,
$n≥2时,{T_n}=-{a_1}+{a_2}+{a_3}+…+{a_n}=S_n^{\;}-2{a_1}=2{n^2}-3n+12$,
综上:n=1时,Tn=11,
n≥2时,${T_n}=2{n^2}-3n+12({n∈{N_+}})$.
点评 本题考查了数列的通项公式的求法,前n项和的定义,属于中档题.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{14}$ | B. | 6 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $2+\sqrt{3}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
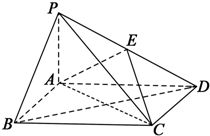 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,$AP=1,AD=\sqrt{3}$,面PAB⊥面ABCD,PA⊥AB,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,$AP=1,AD=\sqrt{3}$,面PAB⊥面ABCD,PA⊥AB,E为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
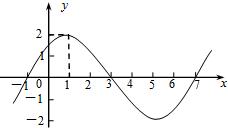 已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2},x∈R)$的图象的一部分如图所示.
已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2},x∈R)$的图象的一部分如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
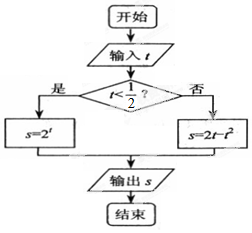
| A. | [0,1] | B. | $[{\frac{3}{4},\sqrt{2}}]$ | C. | $[0,\sqrt{2})$ | D. | $[1,\sqrt{2})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com