
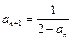 ,(1)求证数列
,(1)求证数列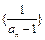 为等差数列,并求出公差;(2)设数列{an}的前n项和为Sn,证明Sn<n-ln(n+1);(3)设
为等差数列,并求出公差;(2)设数列{an}的前n项和为Sn,证明Sn<n-ln(n+1);(3)设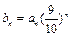 ,证明:对任意正整数n,m,都有
,证明:对任意正整数n,m,都有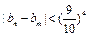 .
.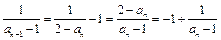 即
即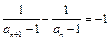 ,∴公差d=-1.
,∴公差d=-1.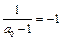 ,故
,故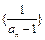 是等差数列.
是等差数列.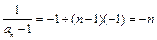 ,∴
,∴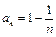 .
.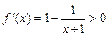 ,f(x)在(0,+∞)↑,且f(x)在[0,+∞)上连续,∴f(x)>f(0)=0,∴x>0时x>ln(x+1), ∴
,f(x)在(0,+∞)↑,且f(x)在[0,+∞)上连续,∴f(x)>f(0)=0,∴x>0时x>ln(x+1), ∴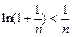 ,即
,即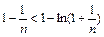 .
.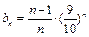 ,∴
,∴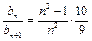 ,当
,当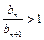 时,则
时,则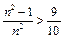 ,∴
,∴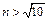 ,
,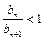 时,则
时,则 ,即n≤3,因此得b1<b2<b3<b4>b5>b6>…,又∵b1=0,n≥2时,bn>0,∴0≤bn≤b4.∴对任意正整数n、m,都有
,即n≤3,因此得b1<b2<b3<b4>b5>b6>…,又∵b1=0,n≥2时,bn>0,∴0≤bn≤b4.∴对任意正整数n、m,都有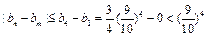


科目:高中数学 来源:不详 题型:解答题
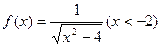 .
.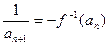 (nÎN+),求{an}的通项公式an;
(nÎN+),求{an}的通项公式an;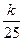 成立.若存在,求出k的值;若不存在,说明理由.
成立.若存在,求出k的值;若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
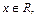 记不超过
记不超过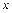 的最大整数为[
的最大整数为[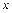 ],令{
],令{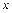 }=
}=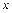 -[
-[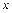 ],则
],则 {
{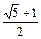 },[
},[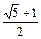 ],
],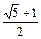 ()
()| A.是等差数列但不是等比数列 | B.是等比数列但不是等差数列 |
| C.既是等差数列又是等比数列 | D.既不是等差数列也不是等比数列 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
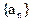 是等和数列且
是等和数列且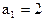 ,公和为5,那么
,公和为5,那么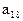 的值为_______,且这个数列前21项和
的值为_______,且这个数列前21项和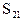 的值为_______。
的值为_______。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com