
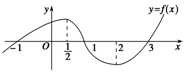
分析 由函数y=f(x)(x∈R)的图象可得函数的单调性,根据单调性与导数的关系得导数的符号,进而得不等式xf′(x)≤0的解集.
解答 解:由f(x)图象特征可得,
f′(x)在(-∞,$\frac{1}{2}$]∪[2,+∞)上大于0,在($\frac{1}{2}$,2)上小于0,
∴xf′(x)≥0?$\left\{\begin{array}{l}{x≥0}\\{f′(x)≥0}\end{array}\right.$或$\left\{\begin{array}{l}{x≤0}\\{f′(x)≤0}\end{array}\right.$?0≤x≤$\frac{1}{2}$或x≥2,
∴xf′(x)≥0的解集为[0,$\frac{1}{2}$]∪[2,+∞).
故答案为:$[0,\frac{1}{2}]∪[2,+∞)$
点评 本题考查导数与函数单调性的关系,考查学生的识图能力,利用导数求函数的单调性是重点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,6] | B. | [3,6] | C. | (3$\sqrt{2}$,6] | D. | [6,9) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x1+x2>0 | B. | x1+x2<0 | C. | x1+x2=0 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等边三角形 | B. | 等腰三角形 | ||
| C. | 等腰三角形或直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
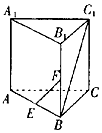 如图所示,在直三棱柱ABC-A1B1C1中,AB=AA1=2,∠ABC=90°,点E、F分别是棱AB、BB1的中点,当二面角C1-AA1-B为45o时,直线EF和BC1所成的角为( )
如图所示,在直三棱柱ABC-A1B1C1中,AB=AA1=2,∠ABC=90°,点E、F分别是棱AB、BB1的中点,当二面角C1-AA1-B为45o时,直线EF和BC1所成的角为( )| A. | 45o | B. | 60o | C. | 90o | D. | 120o |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≥$\frac{5}{2}$ | B. | m>$\frac{5}{2}$ | C. | m≤$\frac{5}{2}$ | D. | m<$\frac{5}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com