
| A. | 0.01 | B. | 0.02 | C. | 0.03 | D. | 0.04 |
分析 根据回归方程$\stackrel{∧}{y}$=2x+1求出对应$\stackrel{∧}{y}$的值,再根据定义计算残差的平方和.
解答 解:根据回归方程$\stackrel{∧}{y}$=2x+1,当x=2时,$\stackrel{∧}{y}$=2×2+1=5,
当x=3时,$\stackrel{∧}{y}$=2×3+1=7,
当x=4时,$\stackrel{∧}{y}$=2×4+1=9;
∴$\stackrel{∧}{{e}_{1}}$=5.1-5=0.1,
$\stackrel{∧}{{e}_{2}}$=6.9-7=-0.1,
$\stackrel{∧}{{e}_{3}}$=9.1-9=0.1;
∴残差平方和为
$\sum_{i=1}^{3}$${\stackrel{∧}{{e}_{i}}}^{2}$=(0.1)2+(-0.1)2+(0.1)2=0.03.
故选:C.
点评 本题考查了变量间的相关关系与回归分析的初步应用问题,是基础题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等边三角形 | B. | 等腰三角形 | ||
| C. | 等腰三角形或直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
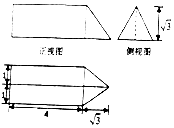
| A. | $4\sqrt{3}+1$ | B. | $4\sqrt{3}$ | C. | $24+2\sqrt{3}+\sqrt{15}$ | D. | $24+3\sqrt{3}+\sqrt{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com