
分析 由题意,f(x)=0,可得m=$\frac{{x}^{2}+x+1}{{e}^{x}}$,确定函数的单调性,结合存在唯一的正整数x0,使得f(x0)≥0,x=1时,m=$\frac{3}{e}$,x=2时,m=$\frac{7}{{e}^{2}}$,即可得出结论
解答 解:由题意,f(x)=0,可得m=$\frac{{x}^{2}+x+1}{{e}^{x}}$,
∴m′=$\frac{-x(x-1)}{{e}^{x}}$,
∴函数在(-∞,0),(1,+∞)上单调递减,在(0,1)上单调递增,
∵存在唯一的正整数x0,使得f(x0)≥0,
x=1时,m=$\frac{3}{e}$,x=2时,m=$\frac{7}{{e}^{2}}$,
∴$\frac{7}{{e}^{2}}$<m≤$\frac{3}{e}$,
故答案为:$({\frac{7}{e^2},\frac{3}{e}}]$;
点评 本题考查特称命题,考查导数知识的运用,考查学生的计算能力,属于中档题


科目:高中数学 来源: 题型:选择题
| A. | $a=\sqrt{3}$ | B. | $a>\sqrt{3}$或$a<-\sqrt{3}$ | C. | $-\sqrt{3}<a<\sqrt{3}$ | D. | $-\sqrt{3}≤a≤\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 济南 | B. | 青岛 | C. | 济南和潍坊 | D. | 济南和青岛 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow a-\overrightarrow b$ | B. | $\overrightarrow b-\overrightarrow a$ | C. | $\overrightarrow b+\overrightarrow a$ | D. | $-\overrightarrow a-\overrightarrow b$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
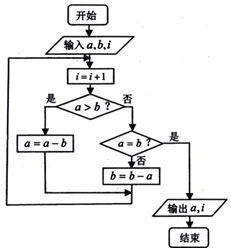 如图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0 时,则输出的i=( )
如图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0 时,则输出的i=( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
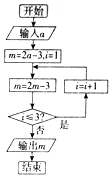 《九章算术》是中国古代数学名著,体现了古代劳动人民数学的智慧,其中第六章“均输”中,有一竹节容量问题,某教师根据这一问题的思想设计了如图所示的程序框图,若输出的m的值为35,则输入的a的值为( )
《九章算术》是中国古代数学名著,体现了古代劳动人民数学的智慧,其中第六章“均输”中,有一竹节容量问题,某教师根据这一问题的思想设计了如图所示的程序框图,若输出的m的值为35,则输入的a的值为( )| A. | 4 | B. | 5 | C. | 7 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
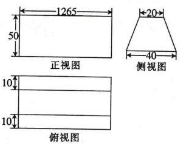 中国古代数学名著《九章算术》卷第五“商功”共收录28个题目,其中一个题目如下:今有城下广四丈,上广二丈,高五丈,袤一百二十六丈五尺,问积几何?其译文可用三视图来解释:某几何体的三视图如图所示(其中侧视图为等腰梯形,长度单位为尺),则该几何体的体积为( )
中国古代数学名著《九章算术》卷第五“商功”共收录28个题目,其中一个题目如下:今有城下广四丈,上广二丈,高五丈,袤一百二十六丈五尺,问积几何?其译文可用三视图来解释:某几何体的三视图如图所示(其中侧视图为等腰梯形,长度单位为尺),则该几何体的体积为( )| A. | 3795000立方尺 | B. | 2024000立方尺 | C. | 632500立方尺 | D. | 1897500立方尺 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在正方形网格中,某四面体的三视图如图所示.如果小正方形网格的边长为1,那么该四面体最长棱的棱长为( )
在正方形网格中,某四面体的三视图如图所示.如果小正方形网格的边长为1,那么该四面体最长棱的棱长为( )| A. | $2\sqrt{5}$ | B. | $4\sqrt{2}$ | C. | 6 | D. | $4\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com