练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．设X～N（6，1），求P（4＜X≤5）．

    分析 根据变量符合正态分布，和所给的μ和σ的值，根据3σ原则，得到P（4＜X≤8）=0.9544，P（5＜X≤7）=0.6826，两个式子相减，根据对称性得到结果．

    解答 解：由已知μ=6，σ=1
    ∵P（μ-2σ＜X≤μ+2σ）=0.9544，P（μ-σ＜X≤μ+σ）=0.6826，μ=6，σ=1，
    ∴P（4＜X≤8）=0.9544，P（5＜X≤7）=0.6826，
    ∴P（4＜X≤8）-P（5＜X≤7）=0.9544-0.6826=0.2718，
    ∴P（4＜X≤5）=$\frac{1}{2}$×0.2718=0.1359．

    点评 本题考查正态分布曲线的特点及曲线所表示的意义，考查正态分布中两个量μ和σ的应用，考查曲线的对称性，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    20．（$\sqrt{x}$+1）6（$\sqrt{x}$-1）4的展开式中x的系数为-3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．如图，在棱长为1的正四面体A-BCD中，平面α与棱AB，AD，CD，BC分别交于点E，F，G，H，则四边形EFGH周长的最小值为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知关于x的不等式|2x-m|≤1的整数解有且仅有一个值为1．
    （Ⅰ）求整数m的值；
    （Ⅱ）已知a，b，c均为正数，若2a+2b+2c=m，求$\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}$的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知$\overrightarrow{a}$，$\overrightarrow{b}$为非零向量，且$\overrightarrow{a}$=（x1，y1），$\overrightarrow{b}$=（x2，y2）则下列命题中与$\overrightarrow{a}⊥\overrightarrow{b}$等价的个数有（　　）
    ①$\overrightarrow{a}•\overrightarrow{b}$=0；②x1x2+y1y2=0；③|$\overrightarrow{a}+\overrightarrow{b}$|2=|$\overrightarrow{a}-\overrightarrow{b}$|2；④${\overrightarrow{a}}^{2}$+$\overrightarrow{b}$2=（$\overrightarrow{a}-\overrightarrow{b}$）2．
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

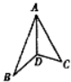    2．在正三角形ABC中，AD⊥BC于D，沿AD折成二面角B-AD-C后，BC=$\frac{1}{2}$AB，这时二面角B-AD-C的大小为60°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知某高级中学高三学生有2000名，在第一次模拟考试中数学成绩ξ服从正态分布N（120，σ2），已知P（100＜?＜120）=0.45．若学校教研室欲按分层抽样的方式从中抽出100份试卷进行分析研究，则应从140分以上的试卷中抽（　　）
    A．4份B．5份C．8份D．10份

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．某城市随机监测一年内100天的空气质量PM2.5的数据API，结果统计如下：
    API[0，50]（50，100]（100，150]（150，200]（200，250]（250，+∞）
    天数61222301416
    （1）若将API值低于150的天气视为“好天”，并将频率视为概率，根据上述表格，预测今年高考6月7日、8日两天连续出现“好天”的概率；
    （2）API值对部分生产企业有着重大的影响，假设某企业的日利润f（x）与API值x的函数关系为：f（x）=$\left\{\begin{array}{l}40（x≤150）\\ 15（x＞150）\end{array}$（单位；万元），利用分层抽样的方式从监测的100天中选出5天，再从这5天中任取3天计算企业利润之和，求利润之和小于80万元的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．计算：log62十21og6$\sqrt{3}$+（0.1）-1=11．

    查看答案和解析>>

    同步练习册答案