Question

5．如图，有一块平行四边形绿地ABCD，经测量BC=2百米，CD=1百米，∠BCD=120°，拟过线段BC上一点E设计一条直路EF（点F在四边形ABCD的边上，不计路的宽度），EF将绿地分成两部分，且右边面积是左边面积的3倍．设EC=x百米，EF=y百米．
（1）当点F与点D重合时，试确定点E的位置；
（2）试求x的值，使直路EF的长度y最短．

Answer 1

分析 （1）当点F与点D重合时，S_△CDE=$\frac{1}{4}$S_ABCD=$\frac{\sqrt{3}}{4}$，代入三角形的面积公式即可确定点E的位置；
（2）分类讨论，确定y关于x的函数关系式，利用配方法求最值．

解答 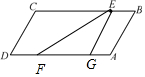解：（1）∵S_ABCD=2S_△BCD=2×1×sin120°=$\sqrt{3}$，
当点F与点D重合时，S_△CDE=$\frac{1}{4}$S_ABCD=$\frac{\sqrt{3}}{4}$，
又∵S_△CDE=$\frac{1}{2}•1•x•sin120°$=$\frac{\sqrt{3}}{4}$x，
∴x=1，即E是BC的中点．
（2）①当点F在CD上，则1≤x≤2时，由S_△CEF=$\frac{1}{2}•x•CF•sin120°$=$\frac{\sqrt{3}}{4}$可得CF=$\frac{1}{x}$，
再由余弦定理可得y=$\sqrt{{x}^{2}+\frac{1}{{x}^{2}}+1}$$≥\sqrt{3}$；当且仅当x=1时取等号，
②当点F在DA上时，则0≤x＜1时，由S_△CEF=$\frac{1}{2}$（x+DF）•1•sin60°=$\frac{\sqrt{3}}{4}$可得DF=1-x，
（ⅰ）当CE＜DF时，过E作EG∥CD交DA于G，在△EGF中，EG=1，GF=1-2x，∠EGF=60°，
利用余弦定理得y=$\sqrt{4{x}^{2}-2x+1}$，
（ⅱ）同理当CE≥DF，过E作EG∥CD交DA于G，在△EGF中，EG=1，GF=2x-1，∠EGF=120°，
利用余弦定理得y=$\sqrt{4{x}^{2}-2x+1}$，
由（ⅰ）、（ⅱ）可得y=$\sqrt{4{x}^{2}-2x+1}$，0≤x＜1
∴y=$\sqrt{4{x}^{2}-2x+1}$=$\sqrt{4（x-\frac{1}{4}）^{2}+\frac{3}{4}}$，
∵0≤x＜1，∴y_min=$\frac{\sqrt{3}}{2}$，当且仅当x=$\frac{1}{4}$时取等号，
由①②可知当x=$\frac{1}{4}$时，路EF的长度最短为$\frac{\sqrt{3}}{2}$．

点评 本题考查了函数在实际问题中的应用及二次函数的性质应用，属于中档题．