练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

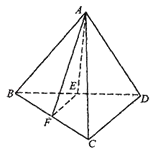
    【题目】如图，正四面体A﹣BCD的棱长为a，点E、F分别是棱BD、BC的中点，则平面AEF截该正四面体的内切球所得截面的面积为_____.

    【答案】

    【解析】

    设圆心为P，内切球的球心为O,内切球的半径为r，作平面,则为底面三角形的中心,由OP⊥AM，可得,,利用相似比求出,利用四面体中的几何关系求出r，再由截面圆的性质可知,所求截面圆的半径求解即可.

    作图如下:

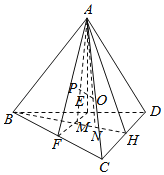
    根据题意知,平面AEF截该正四面体的内切球所得截面一定是圆，

    设圆心为P，内切球的球心为O，

    作平面,则为底面三角形的中心,

    在等边三角形中,,

    在中,由勾股定理知,

    ,

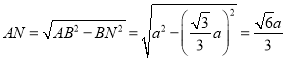    由图可知,为四面体外接球的半径,设,

    在中,由勾股定理可得,

    ,解得，

    所以正四面体A﹣BCD的内切球半径为

    ,

    因为OP⊥AM，,所以，

    又因为，

    由AM2＝NM2+AN2可得AM，

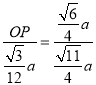    所以，即,解得OP，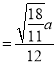

    ∴平面AEF截该正四面体的内切球所得截面圆半径r1，

    平面AEF截该正四面体的内切球所得截面的面积为，

    故答案为:

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知直线l1：x﹣y+3＝0和l2：x+y+1＝0的交点为A，过A且与x轴和y轴都相切的圆的方程为_____，动点B，C分别在l1和l2上，且|BC|＝2，则过A，B，C三点的动圆扫过的区域的面积为_____．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在极标坐系中，已知圆的圆心，半径

    （1）求圆的极坐标方程；

    （2）若，直线的参数方程为（t为参数），直线交圆于两点，求弦长的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （Ⅰ）当时，求函数在上的最值；

    （Ⅱ）讨论函数的单调区间；

    （Ⅲ）当时，对任意，都有恒成立，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，AB为圆O的直径，点E、F在圆O上，ABEF，矩形ABCD所在平面和圆O所在平面垂直，已知AB＝2，EF＝1．

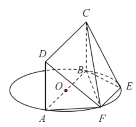
    （I）求证：平面DAF⊥平面CBF；

    （II）若BC＝1，求四棱锥F－ABCD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四棱锥P﹣ABCD中，底面ABCD为平行四边形，点M，N，Q分别在PA，BD，PD上.

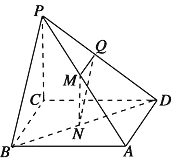
    （1）若PM：MA＝BN：ND＝PQ：QD，求证：平面MNQ∥平面PBC.

    （2）若Q满足PQ：QD＝2，则M点满足什么条件时，BM∥面AQC.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（）的图象在处的切线为（为自然对数的底数）

    （1）求的值；

    （2）若，且对任意恒成立，求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    已知曲线的参数方程为（为参数）.在以坐标原点为极点，轴的正半轴为极轴的极坐标系中，曲线： .

    （Ⅰ）求曲线的普通方程和的直角坐标方程；

    （Ⅱ）若与相交于两点，设点，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国是世界上严重缺水的国家，城市缺水问题较为突出，某市政府为了鼓励居民节约用水，计划在本市试行居民生活用水定额管理，即确定一个合理的居民月用水量标准：（单位：吨），用水量不超过的部分按平价收费，超过的部分按议价收费，为了了解全布市民用用水量分布情况，通过袖样，获得了100位居民某年的月用水量（单位：吨），将数据按照 …… 分成9组，制成了如图所示的频率分布直方图

    （1）求频率分布直方图中的值；

    （2）若该市政府看望使85%的居民每月的用水量不超过标准（吨），估计的值，并说明理由。

    查看答案和解析>>

    同步练习册答案