
【题目】已知平行四边形![]() 中
中![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,三角形
,三角形![]() 为等边三角形,
为等边三角形,![]() ,
,![]() .
.![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 的中点.
的中点.
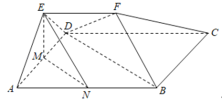
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求直线![]() 与平面
与平面![]() 所成角的正切值.
所成角的正切值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)根据![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 的中点,得到
的中点,得到![]() ,由线面平行的判定定理得到
,由线面平行的判定定理得到![]() 平面
平面![]() ,根据题意得到
,根据题意得到![]() 是平行四边形,有
是平行四边形,有![]() ,由线面平行的判定定理得到
,由线面平行的判定定理得到![]() 平面
平面![]() ,然后由面面平行的判定定理证明.
,然后由面面平行的判定定理证明.
(2)根据平面![]() 平面
平面![]() ,三角形
,三角形![]() 为等边三角形,得到
为等边三角形,得到![]() 平面
平面![]() ,从而有平面
,从而有平面![]() 平面
平面![]() ,根据平面
,根据平面![]() 平面
平面![]() 得证.
得证.
(3)根据平行四边形![]() 中
中![]() ,
,![]() ,易得
,易得![]() ,有
,有![]() 平面
平面![]() ,得到
,得到![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成角,然后在
所成角,然后在![]() 中,求得
中,求得![]() ,得到
,得到![]() ,再由
,再由![]() 求解.
求解.
(1)因为![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 的中点,
的中点,
所以![]() ,
,![]() 平面
平面![]() ,
,
又因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() 是平行四边形,
是平行四边形,
所以![]() ,
,![]() 平面
平面![]() ,
,
又因为![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)平面![]() 平面
平面![]() ,三角形
,三角形![]() 为等边三角形,
为等边三角形,
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
所以平面![]() 平面
平面![]()
因为平面![]() 平面
平面![]()
所以平面![]() 平面
平面![]() ;
;
(3)已知平行四边形![]() 中
中![]() ,
,![]() ,
,
所以![]() ,又平面
,又平面![]() 平面
平面![]() ;
;
所以![]() 平面
平面![]() ,
,
所以![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成角,
所成角,
在![]() 中,
中,![]() ,
,
所以![]() ,
,
所以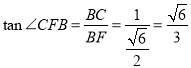 .
.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】火箭少女101的新曲《卡路里》受到了广大听众的追捧,歌词积极向上的体现了人们对于健康以及完美身材的渴望.据有关数据显示,成年男子的体脂率在14%-25%之间.几年前小王重度肥胖,在专业健身训练后,身材不仅恢复正常,且走上美体路线.通过整理得到如下数据及散点图.
健身年数 | 1 | 2 | 3 | 4 | 5 | 6 |
体脂率 | 32 | 20 | 12 | 8 | 6.4 | 4.4 |
| 3.4 | 3 | 2.5 | 2.1 | 1.9 | 1.5 |
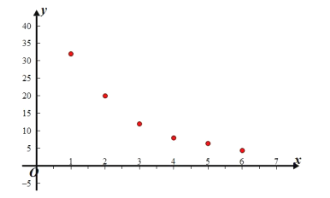
(1)根据散点图判断,![]() 与
与![]() 哪一个模型更适宜作为体脂率关于健身年数的回归方程模型(给出选择即可)
哪一个模型更适宜作为体脂率关于健身年数的回归方程模型(给出选择即可)
(2)根据(1)的判断结果与题目中所给数据,建立![]() 与
与![]() 的回归方程.(保留一位小数)
的回归方程.(保留一位小数)
(3)再坚持3年,体脂率可达到多少.
参考公式: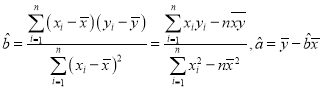
参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在10件产品中,有3件一等品,4件二等品,3件三等品。从这10件产品中任取3件,求:
(I) 取出的3件产品中一等品件数X的分布列和数学期望;
(II) 取出的3件产品中一等品件数多于二等品件数的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某贫困地区几个丘陵的外围有两条相互垂直的直线型公路![]() ,
,![]() ,以及铁路线上的一条应开凿的直线穿山隧道
,以及铁路线上的一条应开凿的直线穿山隧道![]() ,为进一步改善山区的交通现状,计划修建一条连接两条公路
,为进一步改善山区的交通现状,计划修建一条连接两条公路![]() ,
,![]() 和山区边界的直线型公路
和山区边界的直线型公路![]() ,以
,以![]() ,
,![]() 所在的直线分别为
所在的直线分别为![]() 轴,
轴,![]() 轴,建立平面直角坐标系
轴,建立平面直角坐标系![]() ,如图所示,山区边界曲线为
,如图所示,山区边界曲线为![]() ,设公路
,设公路![]() 与曲线
与曲线![]() 相切于点
相切于点![]() .
.
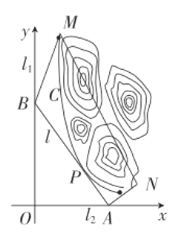
(1)设公路![]() 交
交![]() 轴,
轴,![]() 轴分别为
轴分别为![]() 两点,若公路
两点,若公路![]() 的斜率为-1,求
的斜率为-1,求![]() 的长;
的长;
(2)当公路![]() 的长度最短时,设公路
的长度最短时,设公路![]() 交
交![]() 轴,
轴,![]() 轴分别为
轴分别为![]() ,
,![]() 两点,并测得四边形
两点,并测得四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 千米,
千米,![]() 千米,求应开凿的隧道
千米,求应开凿的隧道![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某部影片的盈利额(即影片的票房收入与固定成本之差)记为![]() ,观影人数记为
,观影人数记为![]() ,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后
,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后![]() 与
与![]() 的函数图象.
的函数图象.
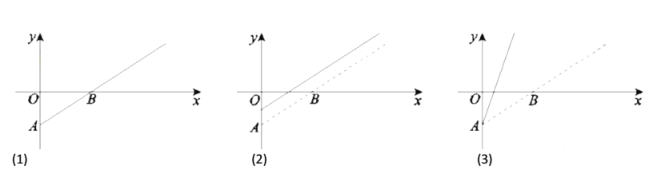
给出下列四种说法:
①图(2)对应的方案是:提高票价,并提高成本;
②图(2)对应的方案是:保持票价不变,并降低成本;
③图(3)对应的方案是:提高票价,并保持成本不变;
④图(3)对应的方案是:提高票价,并降低成本.
其中,正确的说法是____________.(填写所有正确说法的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点![]() 是抛物线
是抛物线![]() 内一点,
内一点,![]() 是抛物线
是抛物线![]() 的焦点,
的焦点,![]() 是抛物线
是抛物线![]() 上任意一点,且已知
上任意一点,且已知![]() 的最小值为2.
的最小值为2.
(1)求抛物线![]() 的方程;
的方程;
(2)抛物线![]() 上一点
上一点![]() 处的切线与斜率为常数
处的切线与斜率为常数![]() 的动直线
的动直线![]() 相交于
相交于![]() ,且直线
,且直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 、
、![]() 两点.问是否有常数
两点.问是否有常数![]() 使
使![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com