
| ��x+�� | 0 | $\frac{��}{2}$ | �� | $\frac{3��}{2}$ | 2�� |
| x | $\frac{��}{2}$ | 2�� | $\frac{7��}{2}$ | 5�� | $\frac{13��}{2}$ |
| f��x�� | 0 | 2 | 0 | -2 | 0 |

���� ��1�����ݦ�x+��=0��$\frac{��}{2}$���У�$\frac{3��}{2}$��2�У���������x������ͼ�ɣ�
��2�����ݡ���㷨��������ͼ�ɣ�
��3������ƽ�Ʊ任�Ĺ��ɼ��ɵõ���
��� �⣺��1����$f��x��=2sin��\frac{1}{3}x-\frac{��}{6}��$��
��$\frac{1}{3}x-\frac{��}{6}$=0ʱ���ɵ�x=$\frac{��}{2}$��f��x��=0��
��$\frac{1}{3}x-\frac{��}{6}$=$\frac{��}{2}$ʱ���ɵ�x=2�У�f��x��=2��
��$\frac{1}{3}x-\frac{��}{6}$=��ʱ���ɵ�x=$\frac{7��}{2}$��f��x��=0��
��$\frac{1}{3}x-\frac{��}{6}$=$\frac{3��}{2}$ʱ���ɵ�x=5�У�f��x��=-2��
��$\frac{1}{3}x-\frac{��}{6}$=2��ʱ���ɵ�x=$\frac{13��}{2}$��f��x��=0��
��ͼ���£�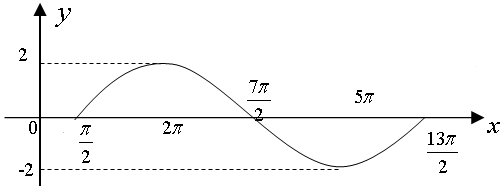
��2��f��x��=sinx��ͼ��仯�õ�$f��x��=2sin��\frac{1}{3}x-\frac{��}{6}��$��ͼ��
��2������f��x��=sinx
��һ����y=sinx$\stackrel{����ƽ��\frac{��}{6}}{��}$y=sin��x-$\frac{��}{6}$��
�ڶ�����y=sin��x-$\frac{��}{6}$��
���������쳤ԭ����3���������겻��ɵ�y=sin��$\frac{1}{3}$x-$\frac{��}{6}$��
��������y=sin��$\frac{1}{3}$x-$\frac{��}{6}$��$\stackrel{�������쳤ԭ����2���������겻��}{��}$y=2sin��$\frac{1}{3}$x-$\frac{��}{6}$��
���� ���⿼�������Ǻ�����ͼ�������ʵ�Ӧ�����⣬����ʱӦ���ݻ����Ǻ�����ͼ��Ļ������軭��ͼ�Σ��ǻ����⣮


 ÿ�α���ϵ�д�
ÿ�α���ϵ�д� ��ѧ����ϵ�д�
��ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | -$\frac{1}{2}$ | C�� | 2 | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{3}$ | B�� | $\frac{2��}{3}$ | C�� | �� | D�� | $\frac{4��}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com