
���� ��������C1�IJ���������ȥ�����������������C1����ͨ���̣�����C2�ļ����귽��չ���ɵæ�sin��+��cos��=8���ɴ����������C2��ֱ�����귽�̣�
��������Բ�ϵĵ�P��$\sqrt{2}cos����sin��$�������õ�P��ֱ�ߵľ��빫ʽ�����Ǻ��������������P������C2�ϵľ������Сֵ��
��� �⣺��������C1�IJ�������Ϊ$\left\{\begin{array}{l}{x=\sqrt{2}cos��}\\{y=sin��}\end{array}\right.$����Ϊ��������
����ȥ��������������C1����ͨ����Ϊ��$\frac{{x}^{2}}{2}+{y}^{2}$=1��
������C2�ļ����귽��$��sin����+\frac{��}{4}��=4\sqrt{2}$��
չ���ɵã�$�ѡ�\frac{\sqrt{2}}{2}$��sin��+cos�ȣ�=4$\sqrt{2}$������sin��+��cos��=8��
������C2��ֱ�����귽��Ϊ��x+y=8������5�֣�
����PΪ����C1�ϵĶ��㣬������Բ�ϵĵ�P��$\sqrt{2}cos����sin��$����
��P��ֱ��O�ľ���Ϊd=$\frac{|\sqrt{2}cos��+sin��-8|}{\sqrt{2}}$=$\frac{|\sqrt{3}sin����+�ȣ�-8|}{\sqrt{2}}$��
�൱sin����+�ȣ�=1ʱ����P������C2�ϵľ������СֵΪdmin=$\frac{8\sqrt{2}-\sqrt{6}}{2}$������10�֣�
���� ���⿼�����ߵ���ͨ���̡�ֱ�����귽�̵�������㵽���ߵľ������Сֵ��������������̡������귽�̡�ֱ�����귽�̵Ļ������㵽ֱ�ߵľ��빫ʽ�Ȼ���֪ʶ������������֤����������������������麯���뷽��˼�룬���е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | S=19+20��T=19��20 | B�� | S=19��20��T=19+20 | ||
| C�� | S=1��2��3������20�� T=1+2+3+��+20 | D�� | S=1+2+3+��+20�� T=1��2��3������20 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | e2x | B�� | e2x-1 | C�� | e2x-2 | D�� | e2x-4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 8 | C�� | 16 | D�� | 18 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{4}{3}$ | B�� | $7+\sqrt{5}$ | C�� | $5+\sqrt{5}$ | D�� | $7+2\sqrt{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
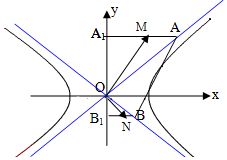 ��ͼ��A��B�ֱ���˫����$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1��a��0��b��0��$���������ϵĵ㣬A��B��y���ϵ���Ӱ�ֱ�ΪA1��B1��M��N�ֱ���A1A��B1B�����е㣬��AB�е���˫�����ϣ���$\overrightarrow{OM}•\overrightarrow{ON}��-{a^2}$����˫���ߵ������ʵ�ȡֵ��ΧΪ��������
��ͼ��A��B�ֱ���˫����$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1��a��0��b��0��$���������ϵĵ㣬A��B��y���ϵ���Ӱ�ֱ�ΪA1��B1��M��N�ֱ���A1A��B1B�����е㣬��AB�е���˫�����ϣ���$\overrightarrow{OM}•\overrightarrow{ON}��-{a^2}$����˫���ߵ������ʵ�ȡֵ��ΧΪ��������| A�� | $��{1��\frac{3}{2}}]$ | B�� | $[\frac{3}{2}��+�ޣ�$ | C�� | $��1��\frac{{\sqrt{5}}}{2}]$ | D�� | $[\frac{{\sqrt{5}}}{2}��+�ޣ�$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com