
| A. | x2-1 | B. | $\frac{1}{x-1}$ | C. | 2x-2 | D. | log2x-2 |
分析 根据函数f(x)的解析式,写出f(|x|)与|f(|x|)|的解析式,
再判断对应方程|f(|x|)|=a在a>0时解的个数.
解答 解:对于A,f(x)=x2-1,∴f(|x|)=x2-1,
∴|f(|x|)|=|x2-1|=$\left\{\begin{array}{l}{1{-x}^{2},-1≤x≤1}\\{{x}^{2}-1,x<-1或x>1}\end{array}\right.$;
方程|f(|x|)|=a,当1>a>0时有4个解,
当a=1时有3个解,当a>1时有2个解,∴A不满足题意;
对于B,f(x)=$\frac{1}{x-1}$,∴f(|x|)=$\frac{1}{|x|-1}$,
∴|f(|x|)|=|$\frac{1}{|x|-1}$|=$\left\{\begin{array}{l}{\frac{1}{|x|-1},|x|>1}\\{\frac{1}{1-|x|},|x|<1}\end{array}\right.$;
方程|f(|x|)|=a,当1>a>0时有2个解,
当a=1时无解,当a>1时有2个解,∴B不满足题意;
对于C,f(x)=2x-2,∴f(|x|)=2|x|-2,
∴|f(|x|)|=|2|x|-2|=$\left\{\begin{array}{l}{2{-2}^{|x|},|x|≤1}\\{{2}^{|x|}-2,|x|>1}\end{array}\right.$;
方程|f(|x|)|=a,当1>a>0时有4个解,
当a=1时有3个解,当a>1时有2个解,∴C不满足题意;
对于D,f(x)=log2x-2,∴f(|x|)=log2|x|-2,
∴|f(|x|)|=|log2|x|-2|=$\left\{\begin{array}{l}{2{-log}_{2}|x|,0<|x|≤4}\\{{log}_{2}|x|-2,|x|>4}\end{array}\right.$;
方程|f(|x|)|=a,当a>0时恒有4个解,∴D满足题意.
故选:D.
点评 本题考查了函数与方程的应用问题,应用函数零点与方程解的关系,是中档题.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:填空题
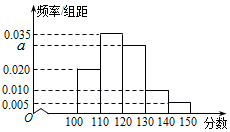 某校从高三年级中随机选取200名学生,将他们的一模数学成绩绘制成频率分布直方图(如图).由图中数据可知a=0.030.若要从成绩在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从成绩在[130,140)内的学生中选取的人数应为4.
某校从高三年级中随机选取200名学生,将他们的一模数学成绩绘制成频率分布直方图(如图).由图中数据可知a=0.030.若要从成绩在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从成绩在[130,140)内的学生中选取的人数应为4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
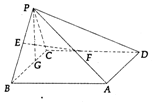 在四棱锥P-ABCD中,底面ABCD为矩形,AB⊥PC,其中BP=BC=3,PC=$\sqrt{6}$
在四棱锥P-ABCD中,底面ABCD为矩形,AB⊥PC,其中BP=BC=3,PC=$\sqrt{6}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16π}{3}$ | B. | $\frac{32π}{3}$ | C. | $\frac{64π}{3}$ | D. | $\frac{128π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com