
分析 求得AM和BN的方程,联立即可求得M坐标,代入椭圆方程,即可求得a,即可求得Γ的离心率.
解答 解:由题意A(0,b),B(0,-b),
则直线AM及BN的方程,$\frac{x}{3}$+$\frac{y}{b}$=1,$\frac{x}{12}$-$\frac{y}{b}$=1,
则$\left\{\begin{array}{l}{\frac{x}{3}+\frac{y}{b}=1}\\{\frac{x}{12}-\frac{y}{b}=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=\frac{24}{5}}\\{y=-\frac{3b}{5}}\end{array}\right.$,则M($\frac{24}{5}$,-$\frac{3b}{5}$),
代入椭圆方程:$\frac{2{4}^{2}}{25{a}^{2}}+\frac{9}{25}=1$,解得:a=6,
由题意的离心率e=$\frac{c}{a}$=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$
点评 本题考查椭圆的简单几何性质,直线的两点式,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 命题“?x0∈R+,x02-x0<0”的否定是“?x∈R-,x2-x≥0” | |
| B. | 命题“若a≠b,则a2≠b2”的否命题是“若a≠b,则a2=b2” | |
| C. | x1>1且x2>1的充要条件是x1+x2>2. | |
| D. | p,q为两个命题,若p∨q为真且p∧q为假,则p,q两个命题中必有一个为真,一个为假. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
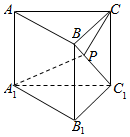 如图,在三棱柱ABC-A1B1C1中,CC1⊥底面A1B1C1,且A1C1⊥B1C1,A1C1=3$\sqrt{2}$,B1C1=CC1=2,P是BC1上一动点,则CP+PA1的最小值为( )
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面A1B1C1,且A1C1⊥B1C1,A1C1=3$\sqrt{2}$,B1C1=CC1=2,P是BC1上一动点,则CP+PA1的最小值为( )| A. | 5$\sqrt{2}$ | B. | 5 | C. | $\sqrt{10}$ | D. | $\sqrt{34}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
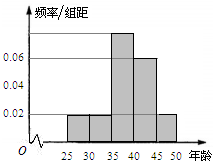 某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.
某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.| 喜欢阅读国学类 | 不喜欢阅读国学类 | 合计 | |
| 男 | 14 | 4 | 18 |
| 女 | 8 | 14 | 22 |
| 合计 | 22 | 18 | 40 |
| 区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50) |
| 人数 | 28 | a | b |
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1-n}{1+n}$ | B. | $\frac{1+n}{1-n}$ | C. | $\frac{n-1}{1+n}$ | D. | $\frac{1+n}{n-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com