
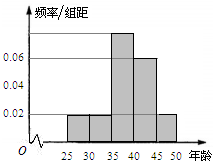
 ij��λN��Ա���μӡ��Ұ��Ķ���������ǵ�������25����50��֮�䣬��������飺��1��[25��30������2��[30��35������3��[35��40������4��[40��45������5��[45��50�����õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
ij��λN��Ա���μӡ��Ұ��Ķ���������ǵ�������25����50��֮�䣬��������飺��1��[25��30������2��[30��35������3��[35��40������4��[40��45������5��[45��50�����õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��| ϲ���Ķ���ѧ�� | ��ϲ���Ķ���ѧ�� | �ϼ� | |
| �� | 14 | 4 | 18 |
| Ů | 8 | 14 | 22 |
| �ϼ� | 22 | 18 | 40 |
| ���� | [25��30�� | [30��35�� | [35��40�� | [40��45�� | [45��50�� |
| ���� | 28 | a | b |
| P��K2��k0�� | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���� ��������Ƶ����Ƶ���Ĺ�ϵ�����������N�������a��b��ֵ��
��������������40���Ա���������÷ֲ����ԭ�����ÿ���ȡ��������
�����ݱ������ݼ���K2�Ĺ۲�ֵ������ó����ʽ��ۣ�
��� �⣺������������$N=\frac{28}{5��0.02}=280$��a=28��
��3���Ƶ���ǣ�1-5����0.02+0.02+0.06+0.02��=0.4
����b=280��0.4=112����4�֣�
������Ϊ�������40���Ա���ڵ�1��2��3�飬����28+28+112=168���ˣ���
���÷ֲ������168���г�ȡ42�ˣ�ÿ���ȡ�������ֱ�Ϊ��
��1���ȡ������Ϊ$28��\frac{42}{168}=7$���ˣ���
��2���ȡ������Ϊ$28��\frac{42}{168}=7$���ˣ���
��3���ȡ������Ϊ$112��\frac{42}{168}=28$���ˣ���
���Ե�1��2��3��ֱ��7�ˡ�7�ˡ�28�ˣ�����8�֣�
������H0�����Ƿ�ϲ������ѧ���鼮���Ա���ϵ�������ݱ������ݣ�
���K2�Ĺ۲�ֵ$k=\frac{{40��{{��14��14-4��8��}^2}}}{22��18��22��18}��6.8605��6.635$��
�����P��K2��6.635��=0.01���Ӷ�����99%�İ�����Ϊ�õ�λԱ���Ƿ�ϲ���Ķ���
ѧ���鼮���Ա��й�ϵ����12�֣�
���� ���⿼����Ƶ�ʷֲ�ֱ��ͼ������Լ����Ӧ�����⣬�ǻ�����Ŀ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 2 | C�� | 1 | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��\frac{{\sqrt{3}}}{6}��\frac{{\sqrt{3}}}{4}]$ | B�� | $��\frac{{\sqrt{3}}}{6}��\frac{{\sqrt{3}}}{4}��$ | C�� | $��\frac{{\sqrt{3}}}{12}��\frac{{\sqrt{3}}}{4}��$ | D�� | $��\frac{{\sqrt{3}}}{12}��\frac{{\sqrt{3}}}{4}]$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com