
分析 根据题意得出四边形ABCD是平行四边形,再利用向量相等列出方程组求出D点的坐标.
解答  解:如图所示,
解:如图所示,
四边形ABCD中,AB∥DC,AD∥BC,
∴四边形ABCD是平行四边形;
又A(0,-2),B(8,6),C(6,8),
设D点坐标为(x,y),
∴$\overrightarrow{AB}$=(8,8),$\overrightarrow{DC}$=(6-x,8-y),
由$\overrightarrow{AB}$=$\overrightarrow{DC}$,得$\left\{\begin{array}{l}{6-x=8}\\{8-y=8}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-2}\\{y=0}\end{array}\right.$,
∴D(-2,0).
故答案为:(-2,0).
点评 本题考查了平面向量的坐标表示与向量相等的应用问题,是基础题目.


 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
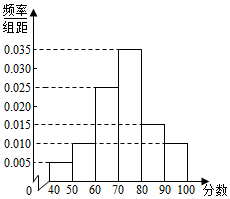 某中学对1000名学生的英语拓展水平测试成绩进行统计,得到样本频率分布直方图如图所示,现规定不低于80分为优秀,则优秀人数是( )
某中学对1000名学生的英语拓展水平测试成绩进行统计,得到样本频率分布直方图如图所示,现规定不低于80分为优秀,则优秀人数是( )| A. | 250 | B. | 200 | C. | 150 | D. | 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com