练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．已知等差数列{an}的前n项和为Sn，且S21=42，若记bn=2${\;}^{{a}_{11}^{2}-{a}_{9}-{a}_{13}}$，则数列{bn}（　　）
    A．是等差数列但不是等比数列B．是等比数列但不是等差数列
    C．既是等差数列又是等比数列D．既不是等差数列又不是等比数列

    分析 根据等差数列的性质和前n项和公式可得a9+a13=4，a11=2，即可得到bn=1，问题得以解决．

    解答 解：S21=42=$\frac{21（{a}_{1}+{a}_{21}）}{2}$=$\frac{21（{a}_{9}+{a}_{13}）}{2}$=$\frac{21×2{a}_{11}}{2}$，
    ∴a9+a13=4，a11=2，
    ∴a112-a9-a13=0，
    ∴bn=2${\;}^{{a}_{11}^{2}-{a}_{9}-{a}_{13}}$=1，
    ∴数列{bn}既是等差数列又是等比数列，
    故选：C

    点评 本题考查了等差数列的性质和前n项和公式，属于中档题

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    5．双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{4}$=1的右焦点到该双曲线渐近线的距离等于（　　）
    A．4B．3C．2$\sqrt{2}$D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{3}，x≤m}\\{{x}^{2}，x＞m}\end{array}\right.$，函数g（x）=f（x）-k．
    （1）当m=2时，若函数g（x）有两个零点，则k的取值范围是（4，8]；
    （2）若存在实数k使得函数g（x）有两个零点，则m的取值范围是（-∞，0）∪（1，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．函数y=lg（cosx-$\frac{\sqrt{3}}{2}$）的定义域为（　　）
    A．（-$\frac{π}{6}$，$\frac{π}{6}$）B．（kπ-$\frac{π}{6}$，kπ+$\frac{π}{6}$）（k∈π）
    C．（2kπ-$\frac{π}{6}$，2kπ+$\frac{π}{6}$）（k∈Z）D．R

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．如图是一个几何体的三视图，则这个几何体的表面积为11+2$\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．设复数z满足z（1+i）=2，i为虚数单位，则复数z的虚部是-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知正数x，y满足x+2y=3，当xy取得最大值时，过点P（x，y）引圆：（x-$\frac{1}{2}$）2+（y+$\frac{1}{4}$）2=$\frac{1}{2}$的切线，则此切线段的长度为$\frac{\sqrt{6}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．有这样一段演绎推理：“指数函数y=ax（a＞0且a≠1）是增函数，而y=（$\frac{1}{2}$）x是指数函数，所以y=（$\frac{1}{2}$）x是增函数”．上面推理显然是错误的，是因为（　　）
    A．大前提错导致结论错B．小前提错导致结论错
    C．推理形式错导致结论错D．大前提和小前提错导致结论错

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

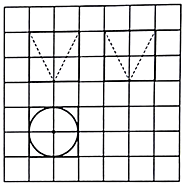    20．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的表面积为（　　）
    A．$20+\sqrt{5}π$B．$24+\sqrt{5}π$C．$20+（\sqrt{5}-1）π$D．$24+（\sqrt{5}-1）π$

    查看答案和解析>>

    同步练习册答案