
| A. | $({\frac{1}{5},\frac{1}{3}})$ | B. | $({\frac{1}{4},\frac{1}{2}})$ | C. | (2,4) | D. | (3,5) |
分析 由题意可得,函数f(x)的图象既关于y轴对称又关于x=1对称,函数f(x)是周期为2,函数y=f(x)的图象
和函数y=logax有的图象有且仅有3个交点,数形结合可得$\left\{\begin{array}{l}{0<a<1}\\{{log}_{a}3>-1}\\{{log}_{a}5<-1}\end{array}\right.$,由此求得a的范围.
解答  解:∵偶函数f(x)满足f(x)=f(2-x),
解:∵偶函数f(x)满足f(x)=f(2-x),
故函数的图象既关于y轴对称又关于x=1对称,
故函数f(x)是周期为2.
由当x∈[-1,0]时,f(x)=cos$\frac{πx}{2}$-1,
可得函数f(x)的图象,
如图所示:
由题意可得,函数y=f(x)的图象
和函数y=logax有的图象有且仅有3个交点,
故有$\left\{\begin{array}{l}{0<a<1}\\{{log}_{a}3>-1}\\{{log}_{a}5<-1}\end{array}\right.$,求得$\frac{1}{5}$<a<$\frac{1}{3}$,
故选:A.
点评 本题主要考查方程根的存在性以及个数判断,体现了转化、数形结合的数学思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
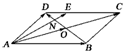 如图,在平行四边形ABCD中,O是对角线AC,BD的交点,N是线段OD的中点,AN的延长线与CD交于点E,若$\overrightarrow{AE}$=m$\overrightarrow{AB}$+$\overrightarrow{AD}$,求实数m的值.
如图,在平行四边形ABCD中,O是对角线AC,BD的交点,N是线段OD的中点,AN的延长线与CD交于点E,若$\overrightarrow{AE}$=m$\overrightarrow{AB}$+$\overrightarrow{AD}$,求实数m的值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(k)+k-1 | B. | f(k)+k+1 | C. | f(k)+k | D. | f(k)+k-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,AB为⊙O的直径,O为圆心,PB与⊙O相切于点B,PO交⊙O于点D,AD的延长线交PB于点C,若AB=2,PB=2$\sqrt{2}$,则BC=$\sqrt{2}$.
如图所示,AB为⊙O的直径,O为圆心,PB与⊙O相切于点B,PO交⊙O于点D,AD的延长线交PB于点C,若AB=2,PB=2$\sqrt{2}$,则BC=$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com