
分析 (1)由奇函数的性质可得f(0)=0,结合条件可得a=1,检验即可;
(2)由题意可得|x-a|≤4+x在x∈[-1,2]时恒成立.即有-4-x≤x-a≤x+4在x∈[-1,2]时恒成立,运用参数分离和一次函数的单调性,可得最值,进而得到a的范围.
解答 解:(1)因为x∈R,若f(x)为奇函数,
则由f(0)=0,得|a|-1=0,
又f(x)不恒为0,得a=1.┉┉┉┉┉┉┉┉┉┉┉┉┉┉(4分)
此时f(-x)=|-x-1|-|-x+1|=-f(x),符合f(x)为奇函数,所以a=1.┉┉┉┉┉┉┉┉┉(5分)
(2)当x∈[-1,2]时,f(x)≤3恒成立,
即|x-a|≤4+x在x∈[-1,2]时恒成立.
故-4-x≤x-a≤x+4在x∈[-1,2]时恒成立,┉┉┉┉┉┉┉┉┉┉┉┉┉(8分)
即-4≤a≤(4+2x)min,x∈[-1,2].
而x∈[-1,2],(4+2x)min=2,所以a的范围是[-4,2].┉┉┉┉┉┉┉┉┉┉┉(10分)
点评 本题考查绝对值函数的性质和不等式恒成立问题解法,注意运用绝对值的含义和参数分离,求最值,考查转化思想,以及运算能力,属于中档题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{4}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
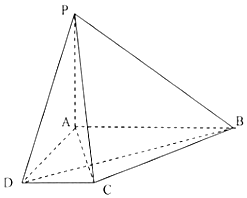 如图,四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,AP=AD=2CD=1,AB=2,PA⊥平面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,AP=AD=2CD=1,AB=2,PA⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\sqrt{3}$) | B. | ($\sqrt{3}$,+∞) | C. | (0,$\sqrt{3}$) | D. | (2,$\sqrt{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间(t) | 2 | 4 | 6 | 8 | 10 |
| 日销售量(y) | 38 | 37 | 32 | 33 | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
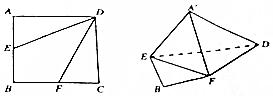 如图,在边长为4的正方形ABCD中,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.
如图,在边长为4的正方形ABCD中,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com