
分析 推导出BG⊥SC,AG⊥SC,∠CEG=30°,取K,F分别为AC、BC的中点,从而得到SA=SC=SB,由此能求出结果.
解答 解:∵三棱锥S-ABC中,△ABC为正三角形,且A在面SBC上的射影H是△SBC的垂心,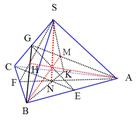
∴S在平面ABC上的射影N是△ABC的垂心,
B在平面SAC上的射影M为△SAC的垂心,
∴BG⊥SC,AG⊥SC,
∵二面角H-AB-C为30°,
∴∠CEG=30°,
又∵△ABC为正三角形,取K,F分别为AC、BC的中点,
又SK⊥AC,SF⊥BC,∴SA=SC=SB,
∴$\frac{SA}{AB}$=$\frac{2\sqrt{3}}{3}$.
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题考查线段比值的求法,解决的关键是对于二面角的求作,以及垂心的运用,得到线段的比值,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 圆台是直角梯形绕其一边旋转而成的旋转体 | |
| B. | 棱台的上下底面一定相似,但侧棱长不一定相等 | |
| C. | 顶点在底面的投影为底面中心的棱锥为正三棱锥 | |
| D. | 圆锥是直角三角形绕其一边旋转而成的旋转体 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
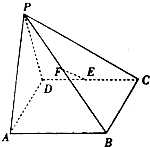 在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,侧面PAD为等边三角形且平面PAD⊥底面ABCD,E、F分别为CD、PB的中点.
在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,侧面PAD为等边三角形且平面PAD⊥底面ABCD,E、F分别为CD、PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
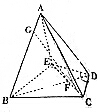 如图所示,在四棱锥A-BCDEE中,AE⊥面BCDE,△BCE是正三角形,BD和CE的交点F恰好平分CE.又AE=BE=2,∠CDE=120°,AG=$\frac{\sqrt{2}}{2}$.
如图所示,在四棱锥A-BCDEE中,AE⊥面BCDE,△BCE是正三角形,BD和CE的交点F恰好平分CE.又AE=BE=2,∠CDE=120°,AG=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
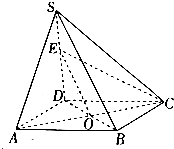 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=2,点E是SD的中点,O是AC与BD的交点.
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=2,点E是SD的中点,O是AC与BD的交点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com