
分析 ①令a=$\frac{1}{2}$,进行验证即可;
②令a=5,通过验证结论成立;
③当a=5时,举反例x=5时,不满足条件;
④求函数的导数,判断函数存在极值进行判断.
解答 解:①当a=$\frac{1}{2}$,则f(x)=x2(lnx-$\frac{1}{2}$)+$\frac{1}{2}$,函数的定义域为(0,+∞),
此时函数的导数f′(x)=2x(lnx-$\frac{1}{2}$)+x2•$\frac{1}{x}$=2xlnx-x+x=2xlnx,
由f′(x)=0得,x=1,则当x>1时,则f′(x)>0,此时函数递增,
当0<x<1时,则f′(x)<0,此时函数递减,故当x=1时,函数f(x)取得极小值同时也是最小值f(1)=-$\frac{1}{2}$+$\frac{1}{2}$=0,
则对?x>0,f(x)≥f(1)=0;故①正确,
②当a=5,则f(x)=x2(lnx-5)+5,则f(e)=e2(lne-5)+5=-4e2+5<0,故②?a>0,?x>0,f(x)≤0,成立.
③由②知当a=5时,?x=e,满足e>0,但f(e)<0,故③?a>0,?x>0,f(x)≥0不成立,故③错误.
④函数的导数f′(x)=2x(lnx-a)+x2•$\frac{1}{x}$=2x(lnx-a)+x=x(2lnx-2a+1)=2x(lnx+$\frac{1}{2}$-a).
由f′(x)=0,则lnx+$\frac{1}{2}$-a=0,即lnx=a-$\frac{1}{2}$,
即?a>0,函数f(x)都存在极值点,即?x>0,f(x)≤0成立,故④正确,
综上正确是有①②④,共3个
故答案为:3
点评 本题主要考查命题的真假判断,利用特殊值法和排除法是解决本题的关键.难度较大.


科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 9 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,某污水处理厂要在一个矩形ABCD的池底水平铺设污水净化管道(直角△EFG,E是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口E是AB的中点,F,G分别落在AD,BC上,且AB=20m,AD=10$\sqrt{3}$m,设∠GEB=θ.
如图,某污水处理厂要在一个矩形ABCD的池底水平铺设污水净化管道(直角△EFG,E是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口E是AB的中点,F,G分别落在AD,BC上,且AB=20m,AD=10$\sqrt{3}$m,设∠GEB=θ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
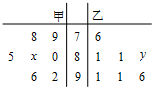 某中学高三文科班从甲、乙两个班各选出7名学生参加文史知识竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是83,则x+y的值为( )
某中学高三文科班从甲、乙两个班各选出7名学生参加文史知识竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是83,则x+y的值为( )| A. | 8 | B. | 7 | C. | 9 | D. | 168 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com