
���� ��1������cos2��+sin2��=1�����ɰ�ԲC�IJ������̻�Ϊֱ�����귽�̣�
��2�������P��Q�ļ����꣬����|PQ|=|��1-��2|���ɵó���
��� �⣺��1������cos2��+sin2��=1����ԲC�IJ�������$\left\{\begin{array}{l}x=1+cos��\\ y=sin��\end{array}\right.$����Ϊ����������Ϊ��x-1��2+y2=1��
���2-2��cos��=0������=2cos�ȣ�
��2���裨��1����1��Ϊ��P�ļ����꣬��P��1��$\frac{��}{3}$����
��ֱ��l�ļ����귽����$2��sin��{��+\frac{��}{3}}��=3\sqrt{3}$���ɵ�Q��3��$\frac{��}{3}$����
��|PQ|=|��1-��2|=2��
���� ���⿼�������ü����귽�������ߵĽ����ҳ���������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{5}{8}$ | B�� | $-\frac{1}{8}$ | C�� | $\frac{1}{8}$ | D�� | $\frac{11}{8}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
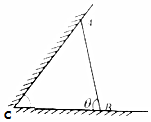 ij����ҪΪ������С���ィ��һ�����濿ǽ��������¶���ң�������״��ͼ��ʾ����֪��������ǽ�ļн�Ϊ$\frac{��}{3}$����ACB=$\frac{��}{3}$����ǽAB�ij���Ϊ6�ף�����������ǽ�Ŀ����ó����㹻���ǡ�ABC=��
ij����ҪΪ������С���ィ��һ�����濿ǽ��������¶���ң�������״��ͼ��ʾ����֪��������ǽ�ļн�Ϊ$\frac{��}{3}$����ACB=$\frac{��}{3}$����ǽAB�ij���Ϊ6�ף�����������ǽ�Ŀ����ó����㹻���ǡ�ABC=���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | 7 | C�� | 8 | D�� | 9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com