
【题目】已知函数f(x)=2|x+1|+|x-2|.
(1)求f(x)的最小值m;
(2)若a,b,c均为正实数,且满足a+b+c=m,求证:![]() +
+![]() +
+![]() ≥3.
≥3.
【答案】(1)m=3 (2)证明见解析
【解析】
(1)分段讨论当x<-1时,当-1≤x<2时,当x≥2时,函数f(x)的值域,然后求函数在定义域上的值域即可;
(2)由已知条件a+b+c=3,再结合重要不等式证明即可.
解:(1)当x<-1时,f(x)=-2(x+1)-(x-2)=-3x∈(3,+∞);
当-1≤x<2时,f(x)=2(x+1)-(x-2)=x+4∈[3,6);
当x≥2时,f(x)=2(x+1)+(x-2)=3x∈[6,+∞).
即![]() ,
,
综上,f(x)的最小值m=3.
(2)证明:因为a,b,c均为正实数,且满足a+b+c=3,
所以![]() +
+![]() +
+![]() +(a+b+c)
+(a+b+c)
=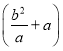 +
+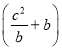 +
+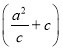
≥2![]()
=2(a+b+c),
当且仅当a=b=c=1时,取“=”,
所以![]() +
+![]() +
+![]() ≥a+b+c,
≥a+b+c,
又a+b+c=3,
即![]() +
+![]() +
+![]() ≥3.
≥3.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称,旨在积极发展我国与沿线国家经济合作关系,共同打造政治互信、经济融合、文化包容的命运共同体.自2013年以来,“一带一路”建设成果显著下图是2013-2017年,我国对“一带一路”沿线国家进出口情况统计图,下列描述正确的是( ).
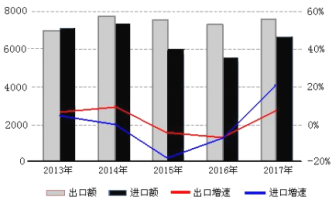
A.这五年,2013年出口额最少
B.这五年,出口总额比进口总额多
C.这五年,出口增速前四年逐年下降
D.这五年,2017年进口增速最快
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 与
与![]() 轴交于
轴交于![]() 两点.以坐标原点
两点.以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 在第一象限交于点
在第一象限交于点![]() ,且线段
,且线段![]() 的中点为
的中点为![]() ,点
,点![]() 在曲线
在曲线![]() 上,求
上,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】田忌赛马是《史记》中记载的一个故事,说的是齐国大将军田忌经常与齐国众公子赛马,孙膑发现田忌的马和其他人的马相差并不远,都分为上、中、下三等.于是孙膑给田忌将军献策:比赛即将开始时,他让田忌用下等马对战公子们的上等马,用上等马对战公子们的中等马,用中等马对战公子们的下等马,从而使田忌赢得了许多赌注.假设田忌的各等级马与某公子的各等级马进行一场比赛,田忌获胜的概率如下表所示:
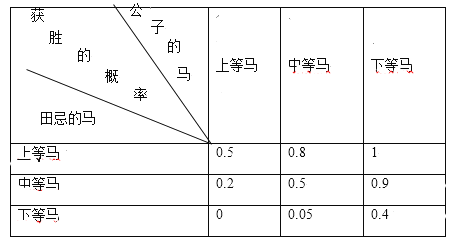
比赛规则规定:一次比赛由三场赛马组成,每场由公子和田忌各出一匹马参赛,结果只有胜和负两种,并且毎一方三场赛马的马的等级各不相同,三场比赛中至少获胜两场的一方为最终胜利者.
(1)如果按孙膑的策略比赛一次,求田忌获胜的概率;
(2)如果比赛约定,只能同等级马对战,每次比赛赌注1000金,即胜利者赢得对方1000金,每月比赛一次,求田忌一年赛马获利的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 是正三角形,CD平面PAD,E,F,G,O分别是PC,PD,BC,AD 的中点.
是正三角形,CD平面PAD,E,F,G,O分别是PC,PD,BC,AD 的中点.

(Ⅰ)求证:PO平面![]() ;
;
(Ⅱ)求平面EFG与平面![]() 所成锐二面角的大小;
所成锐二面角的大小;
(Ⅲ)线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,若存在,求线段
,若存在,求线段![]() 的长度;若不存在,说明理由.
的长度;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电信运营公司为响应国家5G网络建设政策,拟实行5G网络流量阶梯定价.每人月用流量中不超过![]() (一种流量计算单位)的部分按2元
(一种流量计算单位)的部分按2元![]() 收费;超出
收费;超出![]() 的部分按4元
的部分按4元![]() 收费.从用户群中随机调查了10000位用户,获得了他们某月的流量使用数据.整理得到如下的频率分布直方图:
收费.从用户群中随机调查了10000位用户,获得了他们某月的流量使用数据.整理得到如下的频率分布直方图:

(1)若![]() 为整数,依据本次调查,为使80
为整数,依据本次调查,为使80![]() 以上用户在该月的流量价格为2元
以上用户在该月的流量价格为2元![]() ,
,![]() 至少定为多少?
至少定为多少?
(2)假设同组中的每个数据用该组区间的右端点值代替,当![]() 时,试估计用户该月的人均流量费.
时,试估计用户该月的人均流量费.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,分别过
两点,分别过![]() ,
,![]() 作抛物线
作抛物线![]() 的切线,两切线交于点
的切线,两切线交于点![]() .
.
(1)若直线![]() 变动时,点
变动时,点![]() 始终在以
始终在以![]() 为直径的圆上,求动点
为直径的圆上,求动点![]() 的轨迹方程;
的轨迹方程;
(2)设圆![]() ,若直线
,若直线![]() 与圆
与圆![]() 相切于点
相切于点![]() (点
(点![]() 在线段
在线段![]() 上).是否存在点
上).是否存在点![]() 使得
使得![]() ?若存在,求出点
?若存在,求出点![]() 坐标,若不存在,说明理由.
坐标,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com