
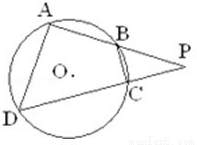
(2010•天津)如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P,若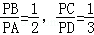 ,则
,则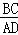 的值为 .
的值为 .
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:[同步]2015人教B版选修4-5 3.2用数学归纳法证明不等式练习卷(解析版) 题型:填空题
用数学归纳法证明1+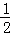 +
+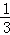 +…+
+…+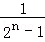 <n(n∈N*,n>1)”时,由n=k(k>1)时,第一步应验证的不等式是 .
<n(n∈N*,n>1)”时,由n=k(k>1)时,第一步应验证的不等式是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习(解析版) 题型:填空题
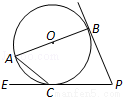
(2014•汕头二模)如图,AB是圆O的直径,PB,PE分别切圆O于B,C,若∠ACE=40°,则∠P= .
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习(解析版) 题型:选择题
如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A,B,与⊙O1分别交于C,D,则APB与CPD的弧长之和为( )
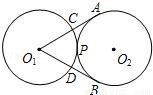
A.2π B.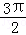 C.π D.
C.π D.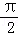
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习(解析版) 题型:选择题
(2010•焦作二模)如图,已知PA为⊙O的切线,PBC为⊙O的割线,PA=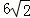 ,PB=BC,⊙O的半径OC=5,那么弦BC的弦心距OM=( )
,PB=BC,⊙O的半径OC=5,那么弦BC的弦心距OM=( )
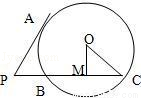
A.4 B.3 C.5 D.6
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理(解析版) 题型:填空题
(2014•泸州三模)在△ABC中,O是其外接圆的圆心,其两条中线的交点是G,两条高线的交点是H,设OG=λGH,则λ的值为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理(解析版) 题型:选择题
圆内接四边形ABCD中,AD∥BC,AC与BD交于点E,在下图中全等三角形的对数为( )
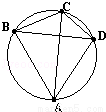
A.2对 B.3对 C.4对 D.5对
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 3.4导数在实际生活中的应用练习卷(解析版) 题型:解答题
如图所示,设铁路AB=50,B、C之间距离为10,现将货物从A运往C,已知单位距离铁路费用为2,公路费用为4,问在AB上何处修筑公路至C,可使运费由A到C最省?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com